
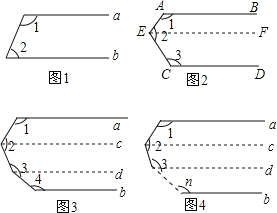
【题目】(1)如图1,a∥b,则∠1+∠2=
(2)如图2,AB∥CD,则∠1+∠2+∠3= ,并说明理由
(3)如图3,a∥b,则∠1+∠2+∠3+∠4=
(4)如图4,a∥b,根据以上结论,试探究∠1+∠2+∠3+∠4+…+∠n= (直接写出你的结论,无需说明理由)

【答案】(1)、180°;(2)、360°;(3)、540°;(4)、(n﹣1)180°
【解析】
试题分析:(1)、根据两直线平行,同旁内角互补得出答案;(2)、过点E作EF∥AB,根据平行线的性质得出答案;(3)、过∠2、∠3的顶点作a的平行线,然后根据平行线的性质得出答案;(4)、过∠2、∠3…的顶点作a的平行线,然后根据平行线的性质得出答案.
试题解析:(1)∵a∥b,
∴∠1+∠2=180°;
(2)过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠1+∠AEF=180°,∠CEF+∠2=180°,
∴∠1+∠AEF+∠CEF+∠2=180°+180°,
即∠1+∠2+∠3=360°;
(3)如图,过∠2、∠3的顶点作a的平行线,
则∠1+∠2+∠3+∠4=180°×3=540°;
(4)如图,过∠2、∠3…的顶点作a的平行线,
则∠1+∠2+∠3+∠4+…+∠n=(n﹣1)180°.


 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】计算:
(1)![]()
(2)![]()
(3)![]()
(4)![]()
(5)(-2![]() )3-(-
)3-(-![]() )·(3
)·(3![]() )2
)2
(6)![]()
(7)(a+3b-2c)(a-3b-2c)
(8)(x-2y)(x+2y)(x2-4y2);
查看答案和解析>>
科目:初中数学 来源: 题型:
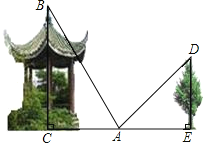
【题目】北京的6月绿树成荫花成海,周末小明约了几个同到户外活动.当他们来到一座小亭子时,一位同学提议测量一下小亭子的高度,大家很高兴.于是设计出了这样一个测量方案:小明在小亭子和一棵小树的正中间点A的位置,观测小亭子顶端B的仰角∠BAC=60°,观测小树尖D的仰角∠DAE=45°.已知小树高DE=2米.请你也参与到这个活动中来,帮他们求出小亭子高BC的长.(结果精确到0.1.![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个三角形的三条高的交点恰好是这个三角形的一个顶点,那么这个三角形是( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
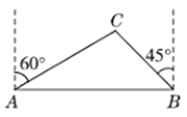
【题目】去年某省将地处A,B两地的两所大学合并成了一所综合性大学,为了方便A,B两地师生的交往,学校准备在相距(1+![]() )km的A,B两地之间修筑一条笔直公路(即图中的线段AB),经测量,在A地的北偏东600方向、B地的西偏北450方向的C处有一个半径为0.7km的公园,问计划修筑的这条公路会不会穿过公园?为什么?
)km的A,B两地之间修筑一条笔直公路(即图中的线段AB),经测量,在A地的北偏东600方向、B地的西偏北450方向的C处有一个半径为0.7km的公园,问计划修筑的这条公路会不会穿过公园?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com