Question

【题目】如图，在△ABC中，M是BC边的中点，AP平分∠A，BP⊥AP于点P、若AB=12，AC=22，则MP的长为_________．

Answer 1

【答案】5

【解析】先作辅助线，再根据三角形全等的性质得出BP=DB，再利用角平分线的性质计算．

解：延长BP与AC相交于D，延长MP与AB相交于E

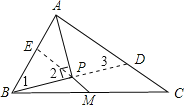
因为∠BAP=∠DAP，AP⊥BD，AP=AP
所以△ABP≌△APD
于是BP=PD
又∵M是BC边的中点
故PM∥AC
所以∠2=∠3
又因为∠1=∠3
所以∠1=∠2，EP=AE=AB=×12=6
AD=2EP=2×6=12
DC=22-12=10
PM=DC=×10=5
故MP的长为5．
故答案为5．

“点睛”本题比较复杂，考查的是三角形的中位线定理及角平分线的性质，解答此题的关键是延长BP与AC相交于D，延长MP与AB相交于E，构造出三角形，再解答．