
如图,在△ABC中,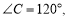
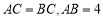 ,半圆的圆心O在AB上,且与AC,BC分别相切于点D, E.
,半圆的圆心O在AB上,且与AC,BC分别相切于点D, E.

(1)求半圆O的半径;
(2)求图中阴影部分的面积.
(1)1;(2)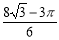 .
.
【解析】
试题分析:(1)连接OC,OD,OE,根据切线的性质得到OD⊥AC,在直角△AOD中,用30°角所对的直角边等于斜边的一半,可以求出半圆的半径.
(2)先在直角△AOC中求出OC的长,计算出△ABC的面积,然后用三角形的面积减去半圆的面积得到阴影部分的面积.
试题解析:(1)【解析】
连结OD, OC,
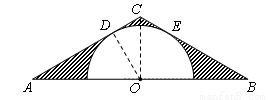
∵半圆与AC,BC分别相切于点D,E
∴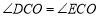 ,且
,且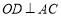
∵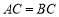 ,
,
∴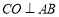 且O是AB的中点
且O是AB的中点
∴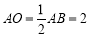
∵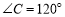 ,∴
,∴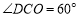
∴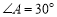
∴在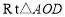 中,
中,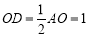
即半圆的半径为1.
(2)设CO=x,则在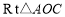 中,因为
中,因为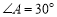 ,所以AC=2x,由勾股定理得:
,所以AC=2x,由勾股定理得:
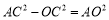
即 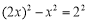
解得 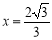 (
(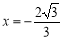 舍去)
舍去)
∴ 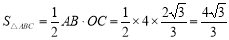 .
.
∵ 半圆的半径为1,
∴ 半圆的面积为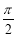 ,
,
∴ 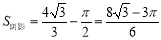 .
.
考点:1.扇形面积的计算;2.切线的性质.


科目:初中数学 来源:[同步]2015年课时同步练习(人教版)八年级数学下册18.1(解析版) 题型:填空题
如图,在□ABCD中,AC⊥AB,∠ABD=30°,AC交BD于O,AO=1,则BC的长为________.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省滕州市九年级上学期期末考试数学试卷(解析版) 题型:解答题
当a>0且x>0时,因为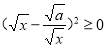 ,所以
,所以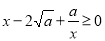 ,从而
,从而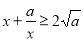 (当x=
(当x=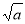 时取等号).记函数
时取等号).记函数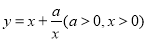 ,由上述结论可知:当x=
,由上述结论可知:当x=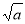 时,该函数有最小值为2
时,该函数有最小值为2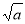
(1)已知函数y1=x(x>0)与函数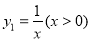 ,则当x= 时,y1+y2取得最小值为
,则当x= 时,y1+y2取得最小值为
(2)已知函数y1=x+1(x>-1)与函数y2=(x+1)2+4(x>1),求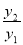 的最小值,并指出取得该最小值时相应的x的值.
的最小值,并指出取得该最小值时相应的x的值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省滕州市九年级上学期期末考试数学试卷(解析版) 题型:选择题
在四边形ABCD中, AC平分∠BAD,且∠ACD=∠B。则下列结论中正确的是
A.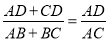 B.
B.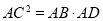
C.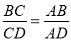 D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省滕州市九年级上学期期末考试数学试卷(解析版) 题型:选择题
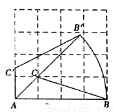
如图,在4×4的正方形网格中,若将△ABC绕着点A逆时针旋转得到△AB′C′,则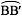 的长为( )
的长为( )
A.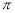 B.
B.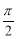 C.7
C.7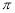 D.6
D.6
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省滕州市九年级上学期期末考试数学试卷(解析版) 题型:填空题
已知P是⊙O外一点,PA切⊙O于A,PB切⊙O于B.若PA=6,则PB= .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年重庆开县七年级上学期期末考试数学试卷(解析版) 题型:选择题
如图所示四个图形中,能用∠α、∠AOB、∠O三种方法表示同一个角的图形是( )

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com