
【题目】厦深铁路开通后,直线l1与l2分别表示从深圳北开往潮阳站的动车和从潮阳站开往深圳的高铁,两车同时出发,设动车离深圳北的距离为y1(千米),高铁离深圳的距离为距离y2(千米),行驶时间为t(小时),与t的函数关系如图所示:
(1)高铁的速度为 km/h;
(2)动车的速度为 km/h;
(3)动车出发多少小时与高铁相遇?
(4)两车出发经过多长时间相距50千米?

【答案】(1)200;(2)150;(3)![]() ;(4)两车出发
;(4)两车出发![]() 小时或1小时时相距50千米.
小时或1小时时相距50千米.
【解析】
(1)根据题意和函数图象中的数据可以求得高铁的速度;
(2)根据题意和函数图象中的数据可以求得动车的速度;
(3)根据函数图象中的数据可以分别求得高铁和动车对应的函数解析式,从而可以解答本题;
(4)根据(3)中的函数解析式,令它们的差的绝对值等于50即可解答本题.
(1)由题意可得:高铁的速度为:300÷1.5=200km/h.
故答案为:200;
(2)由题意可得:动车的速度为:300÷2=150km/h.
故答案为:150;
(3)设动车对应的函数解析式为:y1=kx,则2k=300,得k=150,∴动车对应的函数解析式为:y1=150x,高铁对应的函数解析式为:y2=ax+b,![]() ,得
,得![]() ,即高铁对应的函数解析式为:y2=﹣200x+300,则
,即高铁对应的函数解析式为:y2=﹣200x+300,则![]() ,得
,得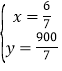 ,即动车出发
,即动车出发![]() 小时与高铁相遇;
小时与高铁相遇;
(4)由题意可得:|150x﹣(﹣200x+300)|=50,解得:x1=![]() ,x2=1,即两车出发
,x2=1,即两车出发![]() 小时或1小时时相距50千米.
小时或1小时时相距50千米.


 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ A=500,∠C=700,BD、BE三等分∠ABC,将△BCE沿BE对折,点C落在C’处,则∠1=_________;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邵阳县某校为了了解学生对语文(A)、数学(B)、英语(C)、物理(D)四科的喜爱程度(每人只选一科),特对八年级某班进行了调查,并绘制成如下频数和频率统计表和扇形统计图.


(1)求出这次调查的总人数;
(2)求出表中a、b、c、d的值;
(3)若该校八年级有学生1000人,请你算出喜爱英语的人数,并发表你的看法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,
(1)试判断DG与BC的位置关系,并说明理由.
(2)若∠A=70°,∠BCG=40°,求∠AGD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由下列条件可判定哪两条直线平行,并说明根据.

(1)∠1=∠2,________________________.
(2)∠A=∠3,________________________.
(3)∠ABC+∠C=180°,________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
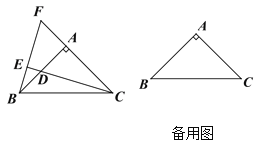
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F
(1)点D在边AB上时,试探究线段BD、AB和AF的数量关系,并证明你的结论;
(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请写出正确结论并证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
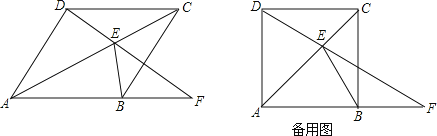
【题目】如图,四边形ABCD为菱形,E为对角线AC上的一个动点,连结DE并延长交射线AB于点F,连结BE.
(1)求证:∠AFD=∠EBC;
(2)若∠DAB=90°,当△BEF为等腰三角形时,求∠EFB的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com