
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F
(1)点D在边AB上时,试探究线段BD、AB和AF的数量关系,并证明你的结论;
(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请写出正确结论并证明。
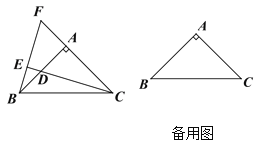
【答案】(1)AB=AF+BD,证明详见解析;(2)不成立,点D在AB的延长线上时,AB=AF-BD;点D在AB的反向延长线上时,AB=BD-AF,证明详见解析.
【解析】
(1)根据已知条件易证△FAB≌△DAC,由全等三角形的性质可得FA=DA,由此即可证得AB=AD+BD=FA+BD;(2)由于点D的位置在变化,因此线段AF、BD、AB之间的大小关系也会相应地发生变化,只需画出图象并借鉴(1)中的证明思路就可解决问题.
(1)AB=FA+BD.
证明:如图,
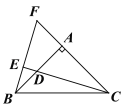
∵BE⊥CD即∠BEC=90°,∠BAC=90°,
∴∠F+∠FBA=90°,∠F+∠FCE=90°.
∴∠FBA=∠FCE.
∵∠FAB=180°-∠DAC=90°,
∴∠FAB=∠DAC.
在△FAB和△DAC中,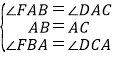 .
.
∴△FAB≌△DAC(ASA).
∴FA=DA.
∴AB=AD+BD=FA+BD.
(2)(1)中的结论不成立.
点D在AB的延长线上时,AB=AF-BD;点D在AB的反向延长线上时,AB=BD-AF.
理由如下:
点D在AB的延长线上时,如图2.
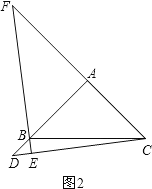
类比(1)的方法可得:FA=DA.
则AB=AD-BD=AF-BD.
②点D在AB的反向延长线上时,如图3.

类比(1)的方法可得:FA=DA.
则AB=BD-AD=BD-AF.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】最近,“校园安全”受到全社会的广泛关注,重庆八中对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如下两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)扇形统计图中“基本了解”部分所对应扇形的圆心角为度;请补全条形统计图;
(2)若达到“了解”程度的人中有1名男生2名女生,达到“不了解”的程度的人中有1名男生和1名女生,若分别从达到“了解”程度和“不了解”的人中分别抽取1人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】厦深铁路开通后,直线l1与l2分别表示从深圳北开往潮阳站的动车和从潮阳站开往深圳的高铁,两车同时出发,设动车离深圳北的距离为y1(千米),高铁离深圳的距离为距离y2(千米),行驶时间为t(小时),与t的函数关系如图所示:
(1)高铁的速度为 km/h;
(2)动车的速度为 km/h;
(3)动车出发多少小时与高铁相遇?
(4)两车出发经过多长时间相距50千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将△ABC平移到△A′B′C′的位置,连接BB′,AA′,CC′,平移的方向是点______到点________的方向,平移的距离是线段______的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
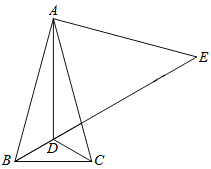
【题目】如图,在△ABC中,AB=AC,∠BAC=30°,点D是△ABC内一点,DB=DC,∠DCB=30°,点E是BD延长线上一点,AE=AB.
(1)求∠ADE的度数;
(2)求证:DE=AD+DC;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,它表示甲乙两人从同一个地点出发后的情况.到十点时,甲大约走了13千米.根据图象回答:
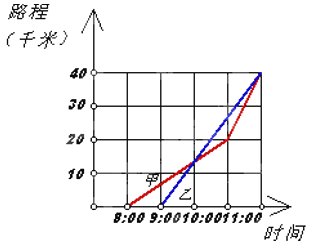
(1)甲是几点钟出发?
(2)乙是几点钟出发,到十点时,他大约走了多少千米?
(3)到十点为止,哪个人的速度快?
(4)两人最终在几点钟相遇?
(5)你能将图象中得到信息,编个故事吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.为了了解全国中学生每天体育锻炼的时间,应采用普查的方式
B.若甲组数据的方差s ![]() =0.03,乙组数据的方差是s
=0.03,乙组数据的方差是s ![]() =0.2,则乙组数据比甲组数据稳定
=0.2,则乙组数据比甲组数据稳定
C.广安市明天一定会下雨
D.一组数据4、5、6、5、2、8的众数是5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店今年1月份购进一批笔记本,共2290本,每本进价为10元,该文具店决定从2月份开始进行销售,若每本售价为11元,则可全部售出;且每本售价每增长0.5元,销量就减少15本.
(1)若该种笔记本在2月份的销售量不低于2200本,则2月份售价应不高于多少元?
(2)由于生产商提高造纸工艺,该笔记本的进价提高了10%,文具店为了增加笔记本的销量,进行了销售调整,售价比中2月份在(1)的条件下的最高售价减少了 ![]() m%,结果3月份的销量比2月份在(1)的条件下的最低销量增加了m%,3月份的销售利润达到6600元,求m的值.
m%,结果3月份的销量比2月份在(1)的条件下的最低销量增加了m%,3月份的销售利润达到6600元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,
上,![]() 射线
射线![]() 绕
绕![]() 点顺时针旋转至
点顺时针旋转至![]() 便立即逆时针回转,射线
便立即逆时针回转,射线![]() 绕
绕![]() 点顺时针旋转至
点顺时针旋转至![]() 便立即逆时针回转.射线
便立即逆时针回转.射线![]() 转动的速度是每秒
转动的速度是每秒![]() 度,射线
度,射线![]() 转动的速度是每秒
转动的速度是每秒![]() 度.
度.

(1)直接写出![]() 的大小为_______;
的大小为_______;
(2)射线![]() 、
、![]() 转动后对应的射线分别为
转动后对应的射线分别为![]() 、
、![]() ,射线
,射线![]() 交直线
交直线![]() 于点
于点![]() ,若射线
,若射线![]() 比射线
比射线![]() 先转动
先转动![]() 秒,设射线
秒,设射线![]() 转动的时间为
转动的时间为![]()
![]() 秒,求
秒,求![]() 为多少时,直线
为多少时,直线![]() 直线
直线![]() ?
?
(3)如图2,若射线![]() 、
、![]() 同时转动
同时转动![]()
![]() 秒,转动的两条射线交于点
秒,转动的两条射线交于点![]() ,作
,作![]() ,点
,点![]() 在
在![]() 上,请探究
上,请探究![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com