
【题目】一组数据3,5,5,4,5,6的众数是 .
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中O是原点,ABCD的顶点A,C的坐标分别是(8,0),(3,4),点D,E把线段OB三等分,延长CD、CE分别交OA、AB于点F,G,连接FG.则下列结论:
①F是OA的中点;②△OFD与△BEG相似;③四边形DEGF的面积是 ![]() ;④OD=
;④OD= ![]()
其中正确的结论是(填写所有正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy,已知二次函数y=﹣![]() x2+bx的图象过点A(4,0),顶点为B,连接AB、BO.
x2+bx的图象过点A(4,0),顶点为B,连接AB、BO.
(1)求二次函数的表达式;
(2)若C是BO的中点,点Q在线段AB上,设点B关于直线CQ的对称点为B',当△OCB'为等边三角形时,求BQ的长度;
(3)若点D在线段BO上,OD=2DB,点E、F在△OAB的边上,且满足△DOF与△DEF全等,求点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:三角形任意两边的“极化值”等于第三边上的中线和这边一半的平方差.如图1,在△ABC中,AO是BC边上的中线,AB与AC的“极化值”就等于AO2﹣BO2的值,可记为AB△AC=AO2﹣BO2 .
(1)在图1中,若∠BAC=90°,AB=8,AC=6,AO是BC边上的中线,则AB△AC= , OC△OA=;
(2)如图2,在△ABC中,AB=AC=4,∠BAC=120°,求AB△AC、BA△BC的值;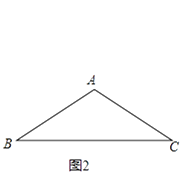
(3)如图3,在△ABC中,AB=AC,AO是BC边上的中线,点N在AO上,且ON= ![]() AO.已知AB△AC=14,BN△BA=10,求△ABC的面积.
AO.已知AB△AC=14,BN△BA=10,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对函数y=﹣2x+2的描述错误是( )
A. y随x的增大而减小 B. 图象与x轴的交点坐标为(1,0)
C. 图象经过第一、三、四象限 D. 图象经过点(3,-4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
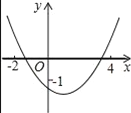
A. c>﹣1 B. b>0 C. 2a+b≠0 D. 9a+c>3b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了增强学生体质,全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用.浠马中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同),绘制了如图两张不完整的人数统计图:

(1)本次被调查的学生有 名;
(2)补全上面的条形统计图1,并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图中所占圆心角的度数;
(3)该校共有1200名学生订购了该品牌的牛奶,牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味要比原味多送多少盒?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com