
【题目】如图(1),点M、N分别是正方形ABCD的边AB、AD的中点,连接CN、DM.
(1)证明:①CN=DM;②CN⊥DM;
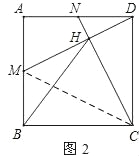
(2)设CN、DM的交点为H,连接BH,如图(2),求证:△BCH是等腰三角形.
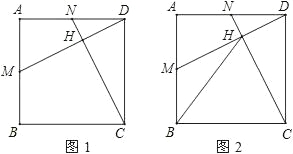
【答案】(1)、证明过程见解析;(2)、证明过程见解析
【解析】
试题分析:(1)、利用正方形的性质可求证△ADM≌△DCN,所以CN=DM,∠ADM=∠DCN,∠ADM+∠CDM=∠DCN+∠CDM=90°,即可求证∠CHD=90°;(2)、连接CM,易证M、B、C、H四点共圆,所以∠BMC=∠BHC,证明△AMD≌△BCM,即可求证∠BHC=∠BCH
试题解析:(1)、由题意知:AD=CD, ∵M、N分别是AB和AD的中点, ∴AM=DN,
在△ADM与△DCN中,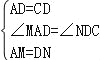 , ∴△ADM≌△DCN(SAS), ∴DM=CN,∠ADM=∠DCN,
, ∴△ADM≌△DCN(SAS), ∴DM=CN,∠ADM=∠DCN,
∴∠DCN+∠CDM=∠ADM+∠CDM=90°, ∴∠CHD=90°, ∴CN⊥DM;
(2)、连接CM, 由(1)可知:∠AMD=90°﹣∠ADM, ∠BCH=90°﹣∠DCN, ∴∠AMD=∠BCH,
∴M、B、C、H四点共圆, ∴∠BMC=∠BHC,
在△BCM与△ADM中,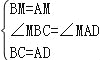 , ∴△BCM≌△ADM(SAS), ∴∠BMC=∠AMD,
, ∴△BCM≌△ADM(SAS), ∴∠BMC=∠AMD,
∴∠BHC=∠AMD=∠BCH, ∴△BCH是等腰三角形


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y1=x2+bx+c的顶点坐标为(﹣1,1),直线1的解析式为y2=2mx+3m2+4nm+4n2,且l与x轴、y轴分别交于A、B两点.
(1)求b、c的值;
(2)若函数y1+y2的图象与x轴始终有公共点,求直线l的解析式;
(3)点P是抛物线对称轴上的一个动点,是否存在点P,使△PAB为等腰角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=30°,AB=AC,以B为圆心,BC长为半径画弧,交AC于点D,交AB于点E.
(1)求∠ABD的度数;
(2)当BC=![]() 时,求线段AE,AD与
时,求线段AE,AD与![]() 围成阴影部分的面积.
围成阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校就“遇见老人摔倒后如何处理”的问题,随机抽取该校部分学生进行问卷调查(每个被调查的学生必须选择而且只能在4种方式中选择一项),图1和图2是整理数据后绘制的两幅不完整的统计图,请根据图中提供的信息,解答下列问题: 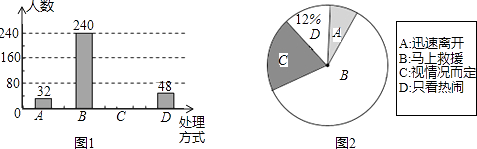
(1)该校随机抽查了名学生;
(2)将图1补充完整,在图2中,“视情况而定”部分所占的圆心角是度;
(3)估计该校2800名学生中采取“马上救助”的方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() ; (2) (-2x)2+(6x3-12x4)÷3x2;
; (2) (-2x)2+(6x3-12x4)÷3x2;
(3) (x+1)2+(2+x)(2-x) ; (4)x(4x+3y)-(2x+y)(2x-y)
(5)![]() (运用公式进行简便计算)
(运用公式进行简便计算)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com