
如图,在正方形ABCD中,点E、F分别是BC、CD的中点,DE交AF于点M,点N为DE的中点.
(1)若AB=4,求△DNF的周长及sin∠DAF的值;
(2)求证:2AD•NF=DE•DM.

(1)△DNF的周长3+ ;sin∠DAF=
;sin∠DAF= ;
;
(2)证明见解析
【解析】
试题分析:(1)由点E、F分别是BC、CD的中点,可求出EC=DF=2,再由勾股定理列式求出DE,然后利用三角形的中位线平行于第三边并且等于第三边的一半求出NF,再求出DN,再根据三角形的周长的定义列式计算即可得解;利用勾股定理列式求出AF,再根据锐角的正弦等于对边比斜边列式计算即可得解;
(2)利用“边角边”证明△ADF和△DCE全等,根据全等三角形对应边相等可得AF=DE,全等三角形对应角相等可得∠DAF=∠CDE,再求出AF⊥DE,然后根据三角形的中位线平行于第三边并且等于第三边的一半可得DF=EC=2NF,然后根据∠DAF和∠CDE的余弦列式整理即可得证.
试题解析:(1)∵点E、F分别是BC、CD的中点,
∴EC=DF= ×4=2,
×4=2,
由勾股定理得,DE= ,
,
∵点F是CD的中点,点N为DE的中点,
∴DN= DE=
DE= =
= ,
,
NF= EC=
EC= ×2=1,
×2=1,
∴△DNF的周长=1+ +2=3+
+2=3+ ;
;
在Rt△ADF中,由勾股定理得,AF= ,
,
所以,sin∠DAF=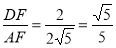 ;
;
(2)在△ADF和△DCE中, ,
,
∴△ADF≌△DCE(SAS),
∴AF=DE,∠DAF=∠CDE,
∵∠DAF+∠AFD=90°,
∴∠CDE+∠AFD=90°,
∴AF⊥DE,
∵点E、F分别是BC、CD的中点,
∴NF是△CDE的中位线,
∴DF=EC=2NF,
∵cos∠DAF= ,
,
cos∠CDE= ,
,
∴ ,
,
∴2AD•NF=DE•DM.
考点:1、正方形的性质;2、勾股定理;3、相似三角形的判定与性质;4、解直角三角形


 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源:2014年初中毕业升学考试(江苏宿迁卷)数学(解析版) 题型:填空题
如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC与BC相交于点D,若BD=4,CD=2,则AB的长是 .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西贺州卷)数学(解析版) 题型:选择题
如图,以AB为直径的⊙O与弦CD相交于点E,且AC=2,AE= ,CE=1.则弧
,CE=1.则弧 的长是( )
的长是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西贺州卷)数学(解析版) 题型:选择题
未来三年,国家将投入8450亿元用于缓解群众“看病难、看病贵”的问题.将8450亿元用科学记数法表示为( )
A.0.845×104亿元 B.8.45×103亿元
C.8.45×104亿元 D.84.5×102亿元
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西河池卷)数学(解析版) 题型:解答题
乔丹体育用品商店开展“超级星期六”促销活动:运动服8折出售,运动鞋每双减20元. 活动期间,标价为480元的某款运动服装(含一套运动服和一双运动鞋)价格为400元.问该款运动服和运动鞋的标价各是多少元?
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西桂林卷)数学(解析版) 题型:选择题
下列命题中,是真命题的是( )
A.等腰三角形都相似 B.等边三角形都相似
C.锐角三角形都相似 D.直角三角形都相似
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com