
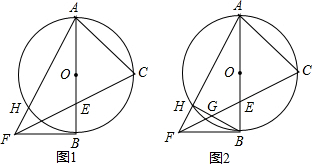
分析 (1)如图1中,连接OC.先证明△COE≌△FBE,推出∠BFE=∠BAF,由OC∥BF,推出∠BFE=∠OCE,再由∠FCA=45°+∠OCE,∠FAC=45°+∠FAB,即可证明∠FAC=∠FCB解决问题.
(2)只要证明BG是Rt△BEF的斜边上的中线即可解决问题.
解答 (1)证明:如图1中,连接OC.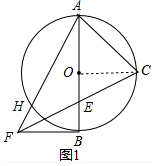
∵AB是直径,
$\widehat{AC}$=$\widehat{BC}$,
∴OC⊥AB,
∵FB是切线,
∴FB⊥AB,
∴∠COE=∠FBE=90°,
∴OC∥BF,
∴∠BFE=∠OCE,
在△COE和△FBE中,
$\left\{\begin{array}{l}{∠COE=∠FBE}\\{OE=EB}\\{∠OEC=∠BEF}\end{array}\right.$,
∴△COE≌△FBE,
∴FB=OC=2OE=2BE,设OE=BE=a,则FB=OC=OB=OA=2a,
∴FB2=BE•BA,
∴$\frac{BF}{BE}$=$\frac{BA}{BF}$,∵∠FBE=∠FBA,
∴△FBE∽△ABF,
∴∠BFE=∠BAF=∠OCE,
∵∠AOC=90°,OA=OC,
∴∠OAC=∠OCA=45°,
∴∠FCA=45°+∠OCE,∠FAC=45°+∠FAB,
∴∠FAC=∠FCB,
∴FC=FA.
(2)解:如图2中,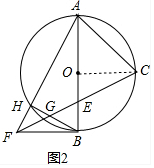
由(1)可知BF=OB=2,BE=OE=1,∠EBF=90°,
∴EF=$\sqrt{B{E}^{2}+B{F}^{2}}$=$\sqrt{5}$,
∵AF是直径,
∴∠AHB=90°,
∴∠FBG+∠ABH=90°,∠ABH+∠BAH=90°,
∴∠FBG=∠BAH=∠GFB,
∴GF=GB,
∵∠BEG+∠BFE=90°,∠EBG+∠FBG=90°,
∴∠BEG=∠GBE,
∴GE=BG=FG=$\frac{1}{2}$EF=$\frac{\sqrt{5}}{2}$,
∴BG=$\frac{\sqrt{5}}{2}$.
点评 本题考查切线的性质、垂径定理、直径的性质、直角三角形斜边中线的性质、全等三角形的判定和性质.相似三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,综合性比较强,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
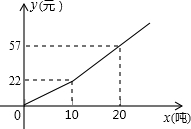 为鼓励市民节约用水,我市自来水公司按分段收费标准收费,右图反映的是每月收取水费y(元)与用水量x(吨)之间的函数关系.下列结论中:
为鼓励市民节约用水,我市自来水公司按分段收费标准收费,右图反映的是每月收取水费y(元)与用水量x(吨)之间的函数关系.下列结论中:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 | 第6列 | … | |
| 第1行 | -2 | 4 | -8 | a | -32 | 64 | … |
| 第2行 | 0 | 6 | -6 | 18 | -30 | 66 | … |
| 第3行 | -1 | 2 | -4 | 8 | -16 | b | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
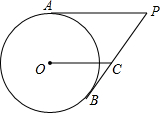 如图,PA,PB分别与⊙O相切于点A,B,OC∥AP交PB于C.
如图,PA,PB分别与⊙O相切于点A,B,OC∥AP交PB于C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com