
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§ΓςABCΒΡ±ΏBC‘Ύ÷±œΏl…œΘ§ACΓΆBCΘ§«“AC=BCΘΜΓςEFPΒΡ±ΏFP“≤‘Ύ÷±œΏl…œΘ§±ΏEF”κ±ΏAC÷ΊΚœΘ§«“EF=FPΘ°
Θ®1Θ© ΨάΐΘΚ‘ΎΆΦ1÷–Θ§Ά®ΙΐΙέ≤λΓΔ≤βΝΩΘ§≤¬œκ≤Δ–¥≥ωAB”κAPΥυ¬ζΉψΒΡ ΐΝΩΙΊœΒΚΆΈΜ÷ΟΙΊœΒΘ°
¥πΘΚAB”κAPΒΡ ΐΝΩΙΊœΒΚΆΈΜ÷ΟΙΊœΒΖ÷±π «ΓΓ ΓΓΓΔΓΓ ΓΓΘ°
Θ®2Θ©ΫΪΓςEFP―Ί÷±œΏlœρΉσΤΫ“ΤΒΫΆΦ2ΒΡΈΜ÷Ο ±Θ§EPΫΜAC”ΎΒψQΘ§Ν§ΫαAPΘ§BQΘ°«κΡψΙέ≤λΓΔ≤βΝΩΘ§≤¬œκ≤Δ–¥≥ωBQ”κAPΥυ¬ζΉψΒΡ ΐΝΩΙΊœΒΚΆΈΜ÷ΟΙΊœΒΘ°¥πΘΚBQ”κAPΒΡ ΐΝΩΙΊœΒΚΆΈΜ÷ΟΙΊœΒΖ÷±π «ΓΓ ΓΓΓΔΓΓ ΓΓΘ°
Θ®3Θ©ΫΪΓςEFP―Ί÷±œΏlœρΉσΤΫ“ΤΒΫΆΦ3ΒΡΈΜ÷Ο ±Θ§EPΒΡ―”≥ΛœΏΫΜACΒΡ―”≥ΛœΏ”ΎΒψQΘ§Ν§ΫαAPΓΔBQΘ°Ρψ»œΈΣΘ®2Θ©÷–Υυ≤¬œκΒΡBQ”κAPΒΡ ΐΝΩΙΊœΒΚΆΈΜ÷ΟΙΊœΒΜΙ≥…ΝΔ¬πΘΩ»τ≥…ΝΔΘ§Ηχ≥ω÷ΛΟςΘΜ»τ≤Μ≥…ΝΔΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©AB=APΘ§ABΓΆAPΘΜΘ®2Θ©BQ=APΘ§BQΓΆAPΘΜΘ®3Θ©≥…ΝΔΘ§÷ΛΟςœξΦϊΫβΈω.
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©”…”ΎACΓΆBCΘ§«“AC=BCΘ§±ΏEF”κ±ΏAC÷ΊΚœΘ§«“EF=FPΘ§‘ρΓςABC”κΓςEFP «»ΪΒ»ΒΡΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§ΗυΨίΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΒΡ–‘÷ ΒΟΒΫΓœBAC=ΓœCAP=45ΓψΘ§AB=APΘ§‘ρΓœBAP=90ΓψΘ§”Ύ «APΓΆABΘΜ
Θ®2Θ©―”≥ΛBOΫΜAP”ΎHΒψΘ§Ω…ΒΟΒΫΓςOPCΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§‘ρ”–OC=PCΘ§ΗυΨίΓΑSASΓ±Ω…≈–ΕœΓςACPΓ’ΓςBCOΘ§‘ρAP=BOΘ§ΓœCAP=ΓœCBOΘ§άϊ”Ο»ΐΫ«–ΈΡΎΫ«ΚΆΕ®άμΩ…ΒΟΒΫΓœAHO=ΓœBCO=90ΓψΘ§Φ¥APΓΆBOΘΜ
Θ®3Θ©BO”κAPΥυ¬ζΉψΒΡ ΐΝΩΙΊœΒΈΣœύΒ»Θ§ΈΜ÷ΟΙΊœΒΈΣ¥Ι÷±Θ°÷ΛΟςΖΫΖ®”κΘ®2Θ©“Μ―υΘ°
‘ΧβΫβΈωΘΚΘ®1Θ©AB=APΘ§ABΓΆAPΘΜ
Θ®2Θ©BQ=APΘ§BQΓΆAPΘΜ
Θ®3Θ©≥…ΝΔΘ°άμ”…»γœ¬ΘΚ
ΓΏΓœEPF=45ΓψΘ§ΓύΓœCPQ=45ΓψΘ°
ΓΏACΓΆBCΘ§ΓύΓœCQP=ΓœCPQΘ§CQ=CPΘ°
‘ΎRtΓςBCQΚΆRtΓςACP÷–Θ§ΓΏBC=ACΘ§ΓœBCQ=ΓœACPΘ§CQ=CPΘ§ΓύRtΓςBCQΓ’RtΓςACPΘ®SASΘ©Θ§
ΓύBQ=APΘΜ
―”≥ΛQBΫΜAP”ΎΒψNΘ§ΓύΓœPBN=ΓœCBQΘ°
ΓΏRtΓςBCQΓ’RtΓςACPΘ§ΓύΓœBQC=ΓœAPCΘ°
‘ΎRtΓςBCQ÷–Θ§ΓΏΓœBCQ+ΓœCBQ=90ΓψΘ§ΓύΓœAPC+ΓœPBN=90ΓψΘ§ΓύΓœPNB=90ΓψΘ§ΓύQBΓΆAPΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈ“Ιζ÷ ΦλΉήΨ÷ΙφΕ®Θ§’κ÷·ΡΎ“¬Β»÷±Ϋ”Ϋ”¥ΞΤΛΖτΒΡ÷ΤΤΖΘ§ΟΩ«ßΩΥΒΡ“¬Έο…œΦΉ»©Κ§ΝΩ”Π‘Ύ0.000075«ßΩΥ“‘œ¬Θ°ΫΪ0.000075”ΟΩΤ―ßΦ« ΐΖ®±μ ΨΈΣΘ® Θ©
A.7.5ΓΝ105
B.7.5ΓΝ10©¹5
C.0.75ΓΝ10©¹4
D.75ΓΝ10©¹6
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩxΒΡ2±Ε”κ3ΒΡ≤ν≤Μ–Γ”Ύ1Θ§Ν–≥ω≤ΜΒ» Ϋ «(ΓΓΓΓ)
A. 2xΘ≠3Γή1 B. 2xΘ≠3Γί1
C. 2xΘ≠3<1 D. 2xΘ≠3>1
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
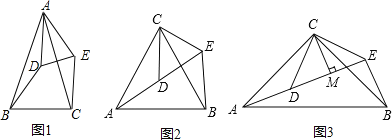
ΓΨΧβΡΩΓΩΘ®1Θ©»γΆΦ1Θ§ΓςABC”κΓςADEΨυ «ΕΞΫ«ΈΣ40ΓψΒΡΒ»―ϋ»ΐΫ«–ΈΘ§BCΓΔDEΖ÷±π «ΒΉ±ΏΘ§«σ÷ΛΘΚBD=CEΘΜ
Θ®2Θ©»γΆΦ2Θ§ΓςACBΚΆΓςDCEΨυΈΣΒ»±Ώ»ΐΫ«–ΈΘ§ΒψAΓΔDΓΔE‘ΎΆ§“Μ÷±œΏ…œΘ§Ν§Ϋ”BEΘ°
ΧνΩ’ΘΚΓœAEBΒΡΕ» ΐΈΣΓΓ ΓΓΘΜœΏΕΈBE”κAD÷°ΦδΒΡ ΐΝΩΙΊœΒ «ΓΓ ΓΓΘ°
Θ®3Θ©ΆΊ’ΙΧΫΨΩ
»γΆΦ3Θ§ΓςACBΚΆΓςDCEΨυΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§ΓœACB=ΓœDCE=90ΓψΘ§ΒψAΓΔDΓΔE‘ΎΆ§“Μ÷±œΏ…œΘ§CMΈΣΓςDCE÷–DE±Ώ…œΒΡΗΏΘ§Ν§Ϋ”BEΘ°«κ≈–ΕœΓœAEBΒΡΕ» ΐΦΑœΏΕΈCMΓΔAEΓΔBE÷°ΦδΒΡ ΐΝΩΙΊœΒΘ§≤ΔΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ‘ΎΧί–ΈABCD÷–Θ§ADΓΈBCΘ§AB=AD=5Θ§tanΓœDBC=![]() Θ°ΒψEΈΣœΏΕΈBD…œ»Έ“β“ΜΒψΘ®ΒψE”κΒψBΘ§D≤Μ÷ΊΚœΘ©Θ§ΙΐΒψEΉςEFΓΈCDΘ§”κBCœύΫΜ”ΎΒψFΘ§Ν§Ϋ”CEΘ°…ηBE=xΘ§y=
Θ°ΒψEΈΣœΏΕΈBD…œ»Έ“β“ΜΒψΘ®ΒψE”κΒψBΘ§D≤Μ÷ΊΚœΘ©Θ§ΙΐΒψEΉςEFΓΈCDΘ§”κBCœύΫΜ”ΎΒψFΘ§Ν§Ϋ”CEΘ°…ηBE=xΘ§y=![]() Θ°
Θ°

Θ®1Θ©«σBDΒΡ≥ΛΘΜ
Θ®2Θ©»γΙϊBC=BDΘ§Β±ΓςDCE «Β»―ϋ»ΐΫ«–Έ ±Θ§«σxΒΡ÷ΒΘΜ
Θ®3Θ©»γΙϊBC=10Θ§«σyΙΊ”ΎxΒΡΚ· ΐΫβΈω ΫΘ§≤Δ–¥≥ωΉ‘±δΝΩxΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ2019ΡξΘ§±ΘΩΒœΊ»ΪΡξΆΕ»κΉ Ϋπ3593Άρ‘ΣΘ§ Β ©―ß–ΘΫ®…ηœνΡΩ16ΗωΘ§–¬Ϋ®ΓΔΗΡά©Ϋ®–Θ…α20398ΤΫΖΫΟΉΘ°Τδ÷–20398m2”ΟΩΤ―ßΦ« ΐΖ®Ω…±μ ΨΈΣΘ® Θ©
A.20.4ΓΝ103m2B.2.03ΓΝ104m2C.2.04ΓΝ104m2D.3.60ΓΝ103Άρ‘Σ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»τ“ΜΗω»ΐΫ«–Έ»ΐΗωΡΎΫ«Ε» ΐΒΡ±»ΈΣ2ΘΚ3ΘΚ4Θ§Ρ«Ο¥’βΗω»ΐΫ«–Έ «Θ® Θ©
A. ÷±Ϋ«»ΐΫ«–Έ B. »ώΫ«»ΐΫ«–Έ
C. ΕέΫ«»ΐΫ«–Έ D. Β»±Ώ»ΐΫ«–Έ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§÷±œΏCD”κ÷±œΏABœύΫΜ”ΎΒψCΘ§ΗυΨίœ¬Ν–”οΨδΜ≠ΆΦΘ®ΉΔΘΚΩ…άϊ”Ο»ΐΫ«≥ΏΜ≠ΆΦΘ§ΒΪ“Σ±Θ≥÷ΆΦ–Έ«εΈζΘ© 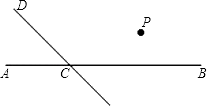
Θ®1Θ©ΙΐΒψPΉςPQΓΈABΘ§ΫΜCD”ΎΒψQΘ§ΙΐΒψPΉςPRΓΆCDΘ§¥ΙΉψΈΣRΘΜ
Θ®2Θ©»τΓœDCB=120ΓψΘ§‘ρΓœQRC «Εύ…ΌΕ»ΘΩ≤ΔΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com