Question

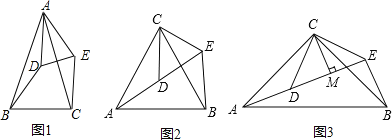
【题目】（1）如图1，△ABC与△ADE均是顶角为40°的等腰三角形，BC、DE分别是底边，求证：BD=CE；

（2）如图2，△ACB和△DCE均为等边三角形，点A、D、E在同一直线上，连接BE．

填空：∠AEB的度数为　 　；线段BE与AD之间的数量关系是　 　．

（3）拓展探究

如图3，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A、D、E在同一直线上，CM为△DCE中DE边上的高，连接BE．请判断∠AEB的度数及线段CM、AE、BE之间的数量关系，并说明理由．

Answer 1

【答案】（1）详见解析；（2）∠AEB的度数为60°；线段BE与AD之间的数量关系是：BE=AD；（3）详见解析.

【解析】试题分析：

(1) 根据已知条件可知，要想证明BD=CE，可以证明△BAD与△CAE全等. 根据已知条件中关于等腰三角形的叙述，可以得到AB=AC，AD=AE. 由于这两个等腰三角形的顶角均为40°，所以这两个顶角分别减去∠DAC也一定相等. 综合上述条件，利用SAS可以证明△BAD与△CAE全等，进而证明BD=CE.

(2) 根据已知条件不难利用SAS证明△ACD和△BCE全等. 利用全等三角形的相关性质，可以得到AD=BE，即线段BE与AD之间的数量关系是BE=AD. 同理，根据全等三角形的性质可知∠ADC=∠BEC. 根据等边三角形的性质和邻补角的相关结论可知，∠BEC=∠ADC=120°. 利用等边三角形的性质即可求得∠AEB的度数.

(3) 通过两个直角与∠DCB的和差关系可以得到∠ACD=∠BCE，再结合等腰直角三角形的性质，不难利用SAS证明△ACD和△BCE全等. 利用全等三角形的性质可以得到AD=BE. 根据等腰直角三角形的性质，可以得到CM=DM=EM. 综上所述，AE=AD+DE=BE+2CM.

试题解析：

(1) 证明：∵∠BAC=∠DAE=40°，

∴∠BAC-∠DAC=∠DAE-∠DAC，即∠BAD=∠CAE.

∵△ABC与△ADE分别是以BC与DE为底边的等腰三角形，

∴AB=AC，AD=AE.

∵在△BAD和△CAE中，

，

∴△BAD≌△CAE (SAS)，

∴BD=CE.

(2) 本小题应依次填写：60°；BE=AD. 理由如下.

∵△ACB和△DCE均为等边三角形，

∴AC=BC，CD=CE，∠ACB=∠DCE=60°.

∴∠ACB-∠DCB=∠DCE-∠DCB，即∠ACD=∠BCE.

∵在△ACD和△BCE中，

，

∴△ACD≌△BCE (SAS)，

∴AD=BE，∠ADC=∠BEC.

∵△DCE为等边三角形，

∴∠CDE=∠CED=60°，

∵点A，D，E在同一直线上，

∴∠ADC=180°-∠CDE=180°-60°=120°，

∴∠BEC=∠ADC=120°，

∴∠AEB=∠BEC-∠CED=120°-60°=60°.

综上所述，∠AEB的度数为60°；线段BE与AD之间的数量关系是：BE=AD.

(3) ∠AEB的度数为90°；线段CM，AE，BE之间的数量关系是：AE=BE+2CM. 理由如下.

∵△ACB和△DCE均为等腰直角三角形且∠ACB=∠DCE=90°，

∴AC=BC，CD=CE，∠CDE=∠CED=45°.

∵∠ACB=∠DCE=90°，

∴∠ACB-∠DCB=∠DCE-∠DCB，即∠ACD=∠BCE.

∵在△ACD和△BCE中，

，

∴△ACD≌△BCE (SAS)，

∴AD=BE，∠ADC=∠BEC，

∵∠CDE=45°，

又∵点A，D，E在同一直线上，

∴∠ADC=180°-∠CDE=180°-45°=135°，

∴∠BEC=∠ADC=135°.

∵∠BEC=135°，∠CED=45°，

∴∠AEB=∠BEC-∠CED=135°-45°=90°.

∵CM为△DCE中DE边上的高，即CM⊥DE，

∴在等腰直角三角形DCE中，DM=EM.

∵CM⊥DE，∠CDE=45°，

∴△CMD是等腰直角三角形，

∴CM=DM.

∴CM=DM=EM.

∵DE=DM+EM=2CM，

又∵AD=BE，

∴AE=AD+DE=BE+2CM.