
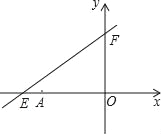
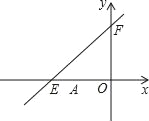
【题目】如图,直线y=kx+6与x轴、y轴分别交于点E、F,点E的坐标为(﹣8,0),点A的坐标为(﹣6,0).
(1)求k的值;
(2)若点P(x,y)是第二象限内的直线上的一个动点,在点P的运动过程中,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)探究:在(2)的情况下,当点P运动到什么位置时,△OPA的面积为![]() ,并说明理由.
,并说明理由.
【答案】(1)k=![]() (2)﹣8<x<0(3)(﹣
(2)﹣8<x<0(3)(﹣![]() ,
, ![]() )
)
【解析】试题分析:(1)将点E坐标(-8,0)代入直线y=kx+6就可以求出k值,从而求出直线的解析式;
(2)由点A的坐标为(-6,0)可以求出OA=6,求△OPA的面积时,可看作以OA为底边,高是P点的纵坐标的绝对值.再根据三角形的面积公式就可以表示出△OPA.从而求出其关系式;根据P点的移动范围就可以求出x的取值范围.
(3)根据△OPA的面积为![]() 代入(2)的解析式求出x的值,再求出y的值就可以求出P点的位置.
代入(2)的解析式求出x的值,再求出y的值就可以求出P点的位置.
(1)∵点E(﹣8,0)在直线y=kx+6上,
∴0=﹣8k+6,
∴k=![]() ;
;
(2)∵k=![]() ,
,
∴直线的解析式为:y=![]() x+6,
x+6,
∵P点在y=![]() x+6上,设P(x,
x+6上,设P(x,![]() x+6),
x+6),
∴△OPA以OA为底的边上的高是|![]() x+6|,
x+6|,
当点P在第二象限时,|![]() x+6|=
x+6|=![]() x+6,
x+6,
∵点A的坐标为(﹣6,0),
∴OA=6.
∴S= =
=![]() x+18.
x+18.
∵P点在第二象限,
∴﹣8<x<0;
(3)设点P(m,n)时,其面积S=![]() ,
,
则![]() ,
,
解得|n|=![]() ,
,
则n1=![]() 或者n2=﹣
或者n2=﹣![]() (舍去),
(舍去),
当n=![]() 时,
时,![]() =
=![]() m+6,
m+6,
则m=﹣![]() ,
,
故P(﹣![]() ,
,![]() )时,三角形OPA的面积为
)时,三角形OPA的面积为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:
①CF=AE;②OE=OF;③图中共有四对全等三角形;④四边形ABCD是平行四边形;其中正确结论的是_____________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)求每套队服和每个足球的价格是多少?
(2)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;
(3)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B两个村庄的坐标分别为(2,2)、(7,4),一辆汽车从原点O出发,在x轴上行驶.
(1)汽车行驶到什么位置时离村庄A最近?写出此位置的坐标.
(2)汽车行驶到什么位置时离村庄B最近?写出此位置的坐标.
(3)请在图中画出汽车到两村庄的距离和最短的位置,并求出此最短的距离和.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是给定△ABC边AB上一动点,D是CP的延长线上一点,且2DP=PC,连结DB,动点P从点B出发,沿BA方向匀速运动到终点A,则△APC与△DBP面积的差的变化情况是( )
A.始终不变
B.先减小后增大
C.一直变大
D.一直变小
查看答案和解析>>
科目:初中数学 来源: 题型:
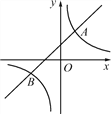
【题目】如图,直线y=k1x+b与双曲线y=![]() 相交于A(1,2)、B(m,-1)两点.
相交于A(1,2)、B(m,-1)两点.
(1)求直线和双曲线的解析式;
(2)若A1(x1,y1)、A2(x2,y2)、A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,请直接写出y1、y2、y3的大小关系式;
(3)观察图象,请直接写出不等式k1x+b>![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为( )

A. ![]() B. 3 C. 1 D.
B. 3 C. 1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E、南门点F分别是AB,AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=里. 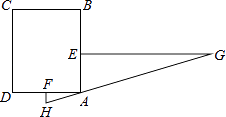
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作;……依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形.如图1,□ABCD中,若AB=1,BC=2,则□ABCD为1阶准菱形.
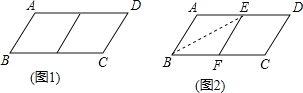
(1)判断与推理:
①邻边长分别为2和3的平行四边形是 阶准菱形;
②小明为了剪去一个菱形,进行如下操作:如图2,把□ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F,得到四边形ABFE.请证明四边形ABEF是菱形.
(2)操作、探究与计算:
①已知□ABCD是邻边长分别为1,a(a>1),且是3阶准菱形,请画出□ABCD及裁剪线的示意图,并在图形下方写出a的值;
②已知□ABCD的邻边长分别为a,b(a>b),满足a=6b+r,b=5r(r>0),则□ABCD
是 阶准菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com