如图.一副三角板如图放置.已知∠2比∠1的补角的2倍小5°.则∠1=145°．题目和参考答案——青夏教育精英家教网—

16．

如图，一副三角板如图放置，已知∠2比∠1的补角的2倍小5°，则∠1=145°．

分析根据三角板的种类，可得∠3=90°，∠4=60°，再由周角为360°即可求得答案．

解答解：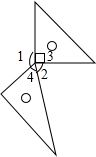

由图形可得：∠3=90°，∠4=60°，
则∠1+∠2=210°，2∠1+∠2=355
又∵∠2比∠1的补角的2倍小5°，
∴可得：$\left\{\begin{array}{l}{∠1+∠2=210°}\\{2（180°-∠1）=∠2+5}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{∠1=145°}\\{∠2=65°}\end{array}\right.$．
故答案为：145°．

点评本题考查了余角和补角的知识，解答本题的关键是熟练三角板的种类，找到隐含条件．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：选择题

6．下列计算正确的是（　　）

A．

a+3a=4a²

B．

a⁴•a⁴=2a⁴

C．

（a²）³=a⁵

D．

（-a）³÷（-a）=a²

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

7．探究问题
（1）阅读操作，在小学阶段我们学过，任何有限位小数都可以转化成分数的形式．
请你将下列各数化成分数形式：
①-3.14=-$\frac{157}{50}$ ②-5.6=-$\frac{28}{5}$
（2）发现问题，我们小学阶段的小数，除有限位小数外，还有无限位的小数，那就是无限循环小数．
（3）提出问题，对于无限循环小数如何将其化成分数的形式？
（4）分析问题：例如：如何将0.$\stackrel{•}{1}\stackrel{•}{4}$化成分数的形式？
分析：假设x=0.$\stackrel{•}{1}\stackrel{•}{4}$，由等式的基本性质得，100x=14.$\stackrel{•}{1}\stackrel{•}{4}$，
即100x=14+0.$\stackrel{•}{1}\stackrel{•}{4}$，也就是100x=14+x，
解这个关于x的一元一次方程，得x=$\frac{14}{99}$，所以0.$\stackrel{•}{1}\stackrel{•}{4}$=$\frac{14}{99}$
说明可以将0.$\stackrel{•}{1}\stackrel{•}{4}$化成分数的形式．
（5）解决问题．请你类比上面的做法，将下列的无限循环小数化成整数或分数的形式：
①0.$\stackrel{•}{9}$=1，②-0.$\stackrel{•}{1}\stackrel{•}{0}$=-$\frac{10}{99}$，③2.$\stackrel{•}{4}0\stackrel{•}{5}$=2$\frac{405}{999}$
（6）归纳结论：整数部分为0的无限循环小数=$\frac{小数部分}{9…（9的个数等于小数部分的数字个数）}$．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

4．下列对平移的描述正确的是（　　）

	A．	坐在秋千上的人的运动是平移
	B．	把一个20°的角向右平移2个单位后度数为40°
	C．	水平线段AB=2cm，向上平移2个单位后得线段CD，则CD∥AB，且CD=2cm
	D．	同一个人手心朝上的两只手，左手可以通过平移与右手重合

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

11．若代数式3a+2b-4的值为2，那么代数式9a+6b-11的值为（　　）

A．

B．

-17

C．

D．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

1．一列匀速行驶的列车在行进途中经过一个长700米的隧道，已知列车从进入隧道到离开隧道共需18秒时间．在这以过程中，坐在该列车上的小王看到身旁的窗口从进入隧道到离开隧道用了14秒时间，求该列车的行驶的速度和列车的长度．

查看答案和解析>>