【题目】某公司销售一种进价为20 （元/个）的计算器，其销售量y （万个）与销售价格x （元/个）之间为一次函数关系，其变化如下表：
价格x （元/个） | … | 30 | 50 | … |
销售量y （万个） | … | 5 | 3 | … |
同时，销售过程中的其他开支（不含进价）总计40万元．若该公司要获得40万元的净利润，且尽可能让顾客得到实惠，那么销售价格应定为多少？
（注：净利润=总销售额﹣总进价﹣其他开支）
科目：初中数学 来源： 题型：
【题目】某玩具店用2000元购进一批玩具，面市后，供不应求，于是店主又购进同样的玩具，所购的数量是第一批数量的3倍，但进价贵了4元，结果购进第二批玩具共用了6300元，若两批玩具的售价都是120元，且两批玩具全部售完，求该玩具店销售这两批玩具共盈利多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，AB=AC，点D是BC的中点，点E是AD上任意一点．
（1）如图1，连接BE、CE，问：BE=CE成立吗？并说明理由；
（2）如图2，若∠BAC=45°，BE的延长线与AC垂直相交于点F时，问：EF=CF成立吗？并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）问题发现
如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE．
填空：①∠AEB的度数为 ；②线段AD，BE之间的数量关系为 ．
（2）拓展探究
如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A，D，E在同一直线上，CM为△DCE中DE边上的高，连接BE，请判断∠AEB的度数及线段CM，AE，BE之间的数量关系，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某通讯公司推出①、②两种通讯收费方式供用户选择，其中一种有月租费，另一种无月租费，且两种收费方式的通讯时间x（分钟）与收费y（元）之间的函数关系如图所示．
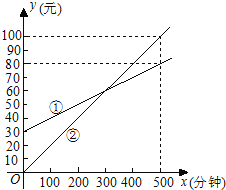
（1）有月租费的收费方式是 （填①或②），月租费是 元；
（2）分别求出①、②两种收费方式中y与自变量x之间的函数关系式；
（3）请你根据用户通讯时间的多少，给出经济实惠的选择建议．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知△ABC中，a、b、c分别是∠A、∠B、∠C的对边，下列条件不能判断△ABC是直角三角形的是（ ）
A. a:b:c＝4:5:6 B. b 2＝a 2－c2 C. ∠A＝∠C－∠B D. a＝3，b=4，c＝5
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】化简，求值
（1）5x2y+{xy﹣[5x2y﹣（7xy2+
xy）]﹣（4x2y+xy）}﹣7xy2，其中x=﹣
，y=﹣16．
（2）A=4x2﹣2xy+4y2，B=3x2﹣6xy+3y2，且|x|=3，y2=16，|x+y|=1，求4A+[（2A﹣B）﹣3（A+B）]的值．
（3）如果m﹣3n+4=0，求：（m﹣3n）2+7m3﹣3（2m3n﹣m2n﹣1）+3（m3+2m3n﹣m2n+n）﹣m﹣10m3的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
