
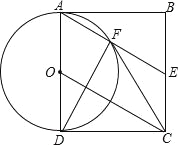
【题目】如图,四边形ABCD为矩形,E为BC边中点,以AD为直径的⊙O与AE交于点F.
(1)求证:四边形AOCE为平行四边形;
(2)求证:CF与⊙O相切;
(3)若F为AE的中点,求∠ADF的大小.
【答案】(1)证明见解析;(2)证明见解析;(3)30°.
【解析】
试题分析:(1)根据矩形的性质得到AD∥BC,AD=BC,∠ADC=90°,由E为BC边中点,AO=DO,得到AO=![]() AD,EC=
AD,EC=![]() BC,等量代换得到AO=EC,AO∥EC,即可得到结论;
BC,等量代换得到AO=EC,AO∥EC,即可得到结论;
(2)利用平行四边形的判定方法得出四边形OAEC是平行四边形,进而得出△ODC≌△OFC(SAS),求出OF⊥CF,进而得出答案;
(3)如图,连接DE,由AD是直径,得到∠AFD=90°,根据点F为AE的中点,得到DF为AE的垂直平分线,根据线段垂直平分线的性质得到DE=AD,推出△ABE≌△DCE,根据全等三角形的性质得到AE=DE,推出三角形ADE为等边三角形,即可得到结论.
试题解析:(1)∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,∠ADC=90°,
∵E为BC边中点,AO=DO,
∴AO=![]() AD,EC=
AD,EC=![]() BC,
BC,
∴AO=EC,AO∥EC,
∴四边形OAEC是平行四边形;
(2)如图1,连接OF,

∵四边形OAEC是平行四边形
∴AE∥OC,
∴∠DOC=∠OAF,
∠FOC=∠OFA,
∵OA=OF,
∴∠OAF=∠OFA,
∴∠DOC=∠FOC,
在△ODC与△OFC中,
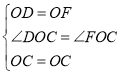 ,
,
∴△ODC≌△OFC(SAS),
∴∠OFC=∠ODC=90°,
∴OF⊥CF,
∴CF与⊙O相切;
(3)如图2,连接DE,
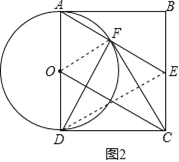
∵AD是直径,
∴∠AFD=90°,
∵点F为AE的中点,
∴DF为AE的垂直平分线,
∴DE=AD,
在△ABE与R△DCE中,
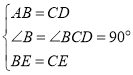 ,
,
∴△ABE≌△DCE,
∴AE=DE,
∴AE=DE=AD,
∴三角形ADE为等边三角形,
∴∠DAF=60°,
∴∠ADF=30°.


科目:初中数学 来源: 题型:
【题目】先化简,再求值.
(1)(a–b)2+b(a–b),其中a=2,b=–![]() .
.
(2)![]() ,其中
,其中![]() ,b=-1.
,b=-1.
(3)(3x+2)(3x-2)-5x(x-1)-(2x-1)2,其中x=-![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论中错误的是( )
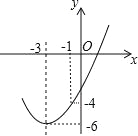
A.b2>4ac
B.ax2+bx+c≥﹣6
C.若点(﹣2,m),(﹣5,n)在抛物线上,则m>n
D.关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD与ECGF是两个边长分别为a,b的正方形,写出用a,b表示阴影部分面积的代数式,并计算当a=4cm,b=6cm时,阴影部分的面积. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com