
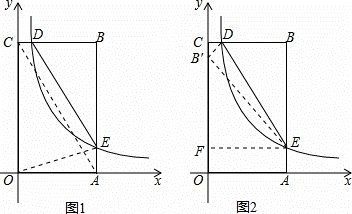
如图,在矩形OABC中,OA=3,OC=5,分别以OA、OC所在直线为x轴、y轴,建立平面直角坐标系,D是边CB上的一个动点(不与C、B重合),反比例函数y=  (k>0)的图象经过点D且与边BA交于点E,连接DE.
(k>0)的图象经过点D且与边BA交于点E,连接DE.
(1)连接OE,若△EOA的面积为2,则k= ;
(2)连接CA,请问DE与CA是否平行?请说明理由;
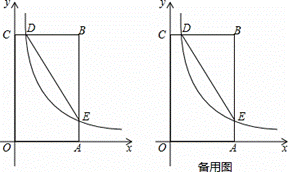 (3)是否存在点D,使得点B关于DE的对称点在OC上?若存在,求出点D的坐标;若不存在,请说明理由.
(3)是否存在点D,使得点B关于DE的对称点在OC上?若存在,求出点D的坐标;若不存在,请说明理由.
解:(1)连接OE,如,图1,
∵Rt△AOE的面积为2, ∴k=2×2=4.………………3分
(2)连接AC,如图1,设D(x,5),E(3,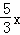 ),则BD=3﹣x,BE=5﹣
),则BD=3﹣x,BE=5﹣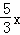 ,
,
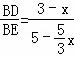 =
=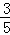 ,
,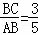
∴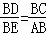 ∴DE∥AC.………………6分
∴DE∥AC.………………6分
(3)假设存在点D满足条件.设D(x,5),E(3,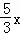 ),则CD=x,
),则CD=x,
BD=3﹣x,BE=5﹣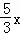 ,AE=
,AE=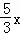 .
.
作EF⊥OC,垂足为F,如图2,
易证△B′CD∽△EFB′,
∴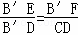 ,即
,即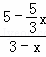 =
=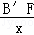 ,
,
∴B′F=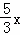 ,
,
∴OB′=B′F+OF=B′F+AE=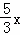 +
+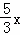 =
=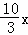 ,
,
∴CB′=OC﹣OB′=5﹣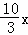 ,
,
在Rt△B′CD中,CB′=5﹣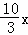 ,CD=x,B′D=BD=3﹣x,
,CD=x,B′D=BD=3﹣x,
由勾股定理得,CB′2+CD2=B′D2,
(5﹣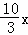 )2+x2=(3﹣x)2,
)2+x2=(3﹣x)2,
解这个方程得,x1=1.5(舍去),x2=0.96,
∴满足条件的点D存在,D的坐标为D(0.96,5).………………10分


科目:初中数学 来源: 题型:
甲、乙两家超市进行促销活动,甲超市采用“买100减50”的促销方式,即购买商品的总金额满100元但不足200元,少付50元;满200元但不足300元,少付100元;….乙超市采用“打6折”的促销方式,即顾客购买商品的总金额打6折.
(1)若顾客在甲商场购买商品的总金额为x(100≤x<200)元,优惠后得到商家的优惠率为p(p=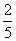 ),写出p与x之间的函数关系式,并说明p随x的变化情况;
),写出p与x之间的函数关系式,并说明p随x的变化情况;
(2)王强同学认为:如果顾客购买商品的总金额超过100元,实际上甲超市采用“打5折”、乙超市采用“打6折”,那么当然选择甲超市购物.请你举例反驳;
(3)品牌、质量、规格等都相同的某种商品,在甲乙两商场的标价都是x(300≤x<400)元,认为选择哪家商场购买商品花钱较少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
从某玉米种子中抽取6批,在同一条件下进行发芽试验,有关数据如下:
| 种子粒数 | 100 | 400 | 800 | 1 000 | 2 000 | 5 000 |
| 发芽种子粒数 | 85 | 398 | 652 | 793 | 1 604 | 4 005 |
| 发芽频率 | 0.850 | 0.745] | 0.851 | 0.793 | 0.802 | 0.801 |
根据以上数据可以估计,该玉米种子发芽的概率约为 (精 确到0.1).
确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
为了解中考体育科目训练情况,长沙市从全市九年级学生中随机抽取了部分学生进行了一次中考体育科目测试(把测试结果分为四个等级:A级:优秀;B级:良 好;C级:及格;D级:不及格),并将测试结果绘成了
好;C级:及格;D级:不及格),并将测试结果绘成了 如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:
如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:
(1)本次抽样测试的学生人数是 ;
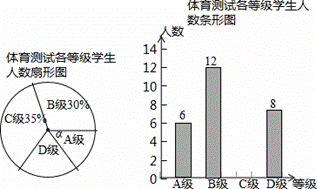 (2)图1中∠α的度数是 ,并把图2条形统计图补充完整;
(2)图1中∠α的度数是 ,并把图2条形统计图补充完整;
(3)若全市九年级有学生35000名,如果全部参加这次中考体育科目测试,请估计不及格的人数为 .
(4)测试老师想从4位同学(分别记为E、F、G、H,其中E为小明)中随机选择两位同学了解平时训练情况,请用列表或画树形图的方法求出选中小明的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
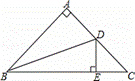
如图,在△ABC中,∠BAC=90°,AB=AC,点D为边AC的中点,DE⊥BC于点E,连接BD,则tan∠DBC的值为( )
A.  B.
B. 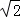 ﹣1 C. 2﹣
﹣1 C. 2﹣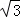 D.
D. 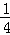
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在⊙O上有顶点C和动点P,位于直径AB的两侧,过点C作CP的垂线与PB的延长线交于点Q,已知⊙O的直径为10,tan∠ABC= ,则CQ最大值为( )
,则CQ最大值为( )
A.5 B. C.
C.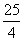 D.
D.
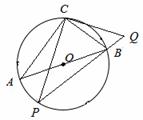
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com