
【题目】(8分)如图,已知直线y=x+k和双曲线y=![]() (k为正整数)交于A,B两点.
(k为正整数)交于A,B两点.
(1)当k=1时,求A、B两点的坐标;
(2)当k=2时,求△AOB的面积;
(3)当k=1时,△OAB的面积记为S1,当k=2时,△OAB的面积记为S2,…,依此类推,当k=n时,△OAB的面积记为Sn,若S1+S2+…+Sn=![]() ,求n的值.
,求n的值.

【答案】(1)A(1,2),B(﹣2,﹣1);(2)4;(3)6.
【解析】试题分析:(1)由k=1得到直线和双曲线的解析式,组成方程组,求出方程组的解,即可得到A、B两点的坐标;(2)先由k=2得到直线和双曲线的解析式,组成方程组,求出方程组的解,即可得到A、B两点的坐标;再求出直线AB的解析式,得到直线AB与y轴的交点(0,2),利用三角形的面积公式,即可解答.(3)根据当k=1时,S1=![]() ×1×(1+2)=
×1×(1+2)=![]() ,当k=2时,S2=
,当k=2时,S2=![]() ×2×(1+3)=4,…得到当k=n时,Sn=
×2×(1+3)=4,…得到当k=n时,Sn=![]() n(1+n+1)=
n(1+n+1)=![]() n2+n,根据若S1+S2+…+Sn=
n2+n,根据若S1+S2+…+Sn=![]() ,列出等式,即可解答.
,列出等式,即可解答.
试题解析:(1)当k=1时,直线y=x+k和双曲线![]() 化为:y=x+1和y=
化为:y=x+1和y= ![]() ,
,
解 得
得![]() ,
, ![]() ,
,
∴A(1,2),B(2,1),
(2)当k=2时,直线y=x+k和双曲线![]() 化为:y=x+2和y=
化为:y=x+2和y=![]() ,
,
解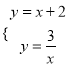 得
得![]() ,
, ![]() ,
,
∴A(1,3),B(3,1)
设直线AB的解析式为:y=mx+n,
∴![]() ,
,
∴![]() ,
,
∴直线AB的解析式为:y=x+2
∴直线AB与y轴的交点(0,2),
∴S△AOB=![]() ×2×1+
×2×1+![]() ×2×3=4;
×2×3=4;
(3)当k=1时,S1=![]() ×1×(1+2)=
×1×(1+2)= ![]() ,
,
当k=2时,S2=![]() ×2×(1+3)=4,
×2×(1+3)=4,
…
当k=n时,Sn=![]() n(1+n+1)=
n(1+n+1)= ![]() n2+n,
n2+n,
∵S1+S2+…+Sn=![]() ,
,
∴![]() ×(12+22+32+…+n2)+(1+2+3+…n)=
×(12+22+32+…+n2)+(1+2+3+…n)= ![]() ,
,
整理得: ![]() ×n(n+1)(2n+1)6+n(n+1)2=
×n(n+1)(2n+1)6+n(n+1)2=![]() ,
,
解得:n=6.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】已知,抛物线![]() ( a≠0)经过原点,顶点为A(h,k)(h≠0).
( a≠0)经过原点,顶点为A(h,k)(h≠0).
(1)当h=1,k=2时,求抛物线的解析式;
(2)若抛物线![]() (t≠0)也经过A点,求a与t之间的关系式;
(t≠0)也经过A点,求a与t之间的关系式;
(3)当点A在抛物线![]() 上,且-2≤h<1时,求a的取值范围.
上,且-2≤h<1时,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
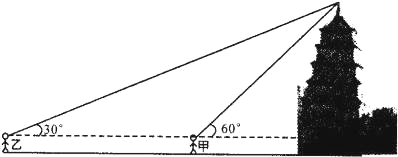
【题目】又到了一年中的春游季节,某班学生利用周末到白塔山去参观“晏阳初博物馆”.下面是两位同学的一段对话:
甲:我站在此处看塔顶仰角为60°;
乙:我站在此处看塔顶仰角为30°;
甲:我们的身高都是1.5m;
乙:我们相距20m.
请你根据两位同学的对话,计算白塔的高度.(精确到1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
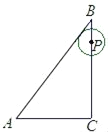
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点P以每秒一个单位的速度沿着B﹣C﹣A运动,⊙P始终与AB相切,设点P运动的时间为t,⊙P的面积为y,则y与t之间的函数关系图象大致是( )
A. 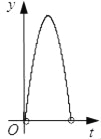 B.
B. 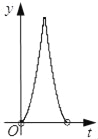 C.
C. 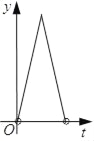 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决“最后一公里一的交通接驳同题,苏州市投放了大量公租自行车供 市民使用到2014年底,全市已有公租自行车25 000辆,租赁点600个,预计到2016年底,全市将有公租自行车50 000辆,并且平均每个租赁点的公租自行车数量是2014年底平均每个租赁点的公租自行车数量的1.2倍,预计到2016年底,全市将有租赁点多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只蚂蚁在一个半圆形的花坛的周边寻找食物,如图1,蚂蚁从圆心![]() 出发,按图中箭头所示的方向,依次匀速爬完下列三条线路:(1)线段
出发,按图中箭头所示的方向,依次匀速爬完下列三条线路:(1)线段![]() 、(2)半圆弧
、(2)半圆弧![]() 、(3)线段
、(3)线段![]() 后,回到出发点.蚂蚁离出发点的距离
后,回到出发点.蚂蚁离出发点的距离![]() (蚂蚁所在位置与
(蚂蚁所在位置与![]() 点之间线段的长度)与时间
点之间线段的长度)与时间![]() 之间的图象如图2所示,问:(注:圆周率
之间的图象如图2所示,问:(注:圆周率![]() 的值取3)
的值取3)
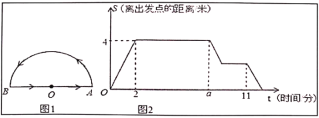
(1)请直接写出:花坛的半径是 米,![]() .
.
(2)当![]() 时,求
时,求![]() 与
与![]() 之间的关系式;
之间的关系式;
(3)若沿途只有一处有食物,蚂蚁在寻找到食物后停下来吃了2分钟,并知蚂蚁在吃食物的前后,始终保持爬行且爬行速度不变,请你求出:
①蚂蚁停下来吃食物的地方,离出发点的距离.
②蚂蚁返回![]() 所用时间.
所用时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
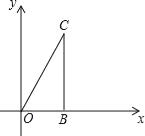
【题目】已知,如图,△OBC中是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=![]() ,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2015C2015,则点C2015的坐标是_____.
,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2015C2015,则点C2015的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题:大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,但是由于1<
的小数部分我们不可能全部地写出来,但是由于1<![]() <2,所以
<2,所以![]() 的整数部分为1,将
的整数部分为1,将![]() 减去其整数部分1,差就是小数部分
减去其整数部分1,差就是小数部分![]() ,根据以上的内容,解答下面的问题:
,根据以上的内容,解答下面的问题:
(1)![]() 的整数部分是______,小数部分是______;
的整数部分是______,小数部分是______;
(2)![]() 的整数部分是______,小数部分是_____;
的整数部分是______,小数部分是_____;
(3)若设![]() 整数部分是x,小数部分是y,求x﹣
整数部分是x,小数部分是y,求x﹣![]() y的值.
y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式,能用平方差公式计算的是( )
A.(2a+b)(2b﹣a)B.(![]() +1)(﹣
+1)(﹣![]() -1)
-1)
C.(2a﹣3b)(﹣2a+3b)D.(﹣a﹣2b)(﹣a+2b)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com