
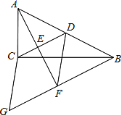
【题目】如图,在![]() 中,
中,![]() ,
,![]() 为
为![]() 边上的中线,过点
边上的中线,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 平行线,交
平行线,交![]() 的延长线于点
的延长线于点![]() ,在延长线上截得
,在延长线上截得![]() ,连结
,连结![]() 、
、![]() .若
.若![]() ,
,![]() ,则四边形
,则四边形![]() 的面积等于________.
的面积等于________.
【答案】![]()
【解析】
首先可判断四边形CGFD是平行四边形,再由直角三角形斜边中线等于斜边一半,可得BD=FD,则可判断四边形CGFD是菱形,CD∥BF,D为AB中点,E为AF的中点,得EF的长,设GF=x,则BF=11-x,AB=2x,在RT△ABF中利用勾股定理可求出x的值.
: ∵∠ACB=90°,CD为AB边上的中线,
∴AD=BD=CD,
∵BG∥CD,
∴AF⊥BG,
∴AD=BD=DF,
∴DF=CD,
∵FG=CD,
∴四边形CGFD为菱形,
∵CD∥BF,D为AB中点,
∴E为AF的中点,
∴EF=![]() AF=4,
AF=4,
设GF=x,则BF=11-x,AB=2x,
∵在RT△ABF中, ∠BFA=90°,
∴AF+BF=AB,即(11-x)+8=(2x),
解得:x=5或x=-![]() (舍去),
(舍去),
∴菱形CGFD的面积为:5×4=20,
故答案为:20.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共4只,某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如表是活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1 000 |
摸到白球的次数m | 28 | 34 | 48 | 130 | 197 | 251 |
摸到白球的频率 | 0.28 | 0.23 | 0.24 | 0.26 | 0.246 | 0.251 |
(1)请估计:当n很大时,摸到白球的频率将会接近 (精确到0.01);
(2)试估算口袋中白种颜色的球有多少只?
(3)请根据估算的结果思考从口袋中先摸出一球,不放回,再摸出一球,这两只球颜色不同的概率是多少?画出树状图(或列表)表示所有可能的结果,并计算概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE.
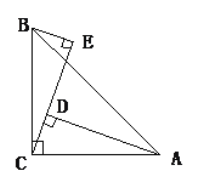
(1)求证:△ACD≌△CBE.
(2)若AD=6.8,DE=4.5,求BE的长度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形网格中,每个小格的顶点叫做格点.当所作正方形边上的点刚好在格点上的点称为整点.如图中![]() 四条边上的整点共有
四条边上的整点共有![]() 个;
个;![]() 四条边上的整点共有
四条边上的整点共有![]() 个.请你观察图中正方形
个.请你观察图中正方形![]() 四条边上的整点的个数…按此规律,推算出正方形
四条边上的整点的个数…按此规律,推算出正方形![]() 四条边上的整点共有________个.
四条边上的整点共有________个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店以固定进价一次性购进一种商品,3月份按一定售价销售,销售额为2400元,为扩大销量,减少库存,4月份在3月份售价基础上打9折销售,结果销售量增加30件,销售额增加840元.
(1)求该商店3月份这种商品的售价是多少元?
(2)如果该商店3月份销售这种商品的利润为900元,那么该商店4月份销售这种商品的利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一元二次方程ax2+bx+c=0(a≠0)的两根是x1、x2,那么利用公式法写出两个根x1、x2,通过计算可以得出:x1+x2=![]() ,x1x2=
,x1x2=![]() .由此可见,一元二次方程两个根的和与积是由方程的系数决定的.这就是一元二次方程根与系数的关系.
.由此可见,一元二次方程两个根的和与积是由方程的系数决定的.这就是一元二次方程根与系数的关系.
请利用上述知识解决下列问题:
(1)若方程2x2-4x-1=0的两根是x1、x2,则x1+x2=__________,x1x2=__________.
(2)已知方程x2-4x+c=0的一个根是![]() ,请求出该方程的另一个根和c的值.
,请求出该方程的另一个根和c的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com