
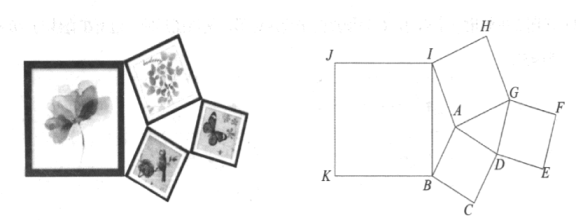
【题目】由四个正方形相框拼成的照片墙如图所示,已知正方形![]() ,正方形
,正方形![]() ,正方形
,正方形![]() 的.面积分别为
的.面积分别为![]() 平方分米,
平方分米,![]() 平方分米,
平方分米,![]() 平方分米,则正方形
平方分米,则正方形![]() 的面积为__________平方分米.
的面积为__________平方分米.
【答案】6
【解析】
作出如图的辅助线,证得![]() ,继而推出
,继而推出![]() ,在Rt△IBQ和Rt△ABQ中,设参数利用勾股定理即可求解.
,在Rt△IBQ和Rt△ABQ中,设参数利用勾股定理即可求解.
如图:作AM⊥BI于M,延长MA交DG于N,分别过D、G作MN的垂线垂足分别为R、S,

∴∠RDN=∠SGN,
∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90![]() ,
,
∴∠MBA+∠MAB=90![]() ,∠RAD+∠MAB=90
,∠RAD+∠MAB=90![]() ,
,
∴∠MBA=∠RAD,
在Rt△MBA和Rt△RAD中,
 ,
,
∴Rt△MBA![]() Rt△RAD,
Rt△RAD,
∴AM=DR,
同理可证得,Rt△MIA![]() Rt△SAG,
Rt△SAG,
∴AM=GS,
∴DR=GS,
在Rt△RDN和Rt△SGN中,
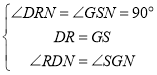 ,
,
∴Rt△RDN![]() Rt△SGN,
Rt△SGN,
∴![]() ;
;
作DP⊥AG于P,作BQ⊥IA交IA延长线于Q,如图:

∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在Rt△ABQ和Rt△ADP中,
![]() ,AB=AD,
,AB=AD,
∴Rt△ABQ![]() Rt△ADP(HL),
Rt△ADP(HL),
∴AQ =AP,
设正方形AGHI的边长为![]() ,
,
由题意,![]() ,DA=DG=
,DA=DG=![]() ,
,![]() ,AP=PG=
,AP=PG=![]() ,AQ =AP
,AQ =AP![]() ,
,
在Rt△IBQ和Rt△ABQ中,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴正方形AGHI的面积为:![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
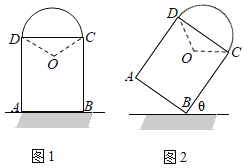
【题目】图1为一艺术拱门,下部为矩形ABCD,AB、AD的长分别为![]() m和4m,上部是圆心为O的劣弧CD,∠COD=120°.现欲以点B为支点将拱门放倒,放倒过程中矩形ABCD所在的平面始终与地面垂直,如图2所示.设BC与地面水平线所成的角为
m和4m,上部是圆心为O的劣弧CD,∠COD=120°.现欲以点B为支点将拱门放倒,放倒过程中矩形ABCD所在的平面始终与地面垂直,如图2所示.设BC与地面水平线所成的角为![]() ,记拱门上的点到地面的距离为h,当h取最大值时,此时
,记拱门上的点到地面的距离为h,当h取最大值时,此时![]() 为________°.
为________°.
查看答案和解析>>
科目:初中数学 来源: 题型:
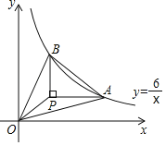
【题目】如图,A、B是函数y=![]() 上两点,P为一动点,作PB∥y轴,PA∥x轴,下列说法:①△AOP≌△BOP;②S△AOP=S△BOP;③若OA=OB,则OP平分∠AOB;④若S△BOP=2,则S△ABP=4,正确有____(填序号)
上两点,P为一动点,作PB∥y轴,PA∥x轴,下列说法:①△AOP≌△BOP;②S△AOP=S△BOP;③若OA=OB,则OP平分∠AOB;④若S△BOP=2,则S△ABP=4,正确有____(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:![]() ,
,![]() ,
,![]() ,将以上三个等式两边分别相加得:
,将以上三个等式两边分别相加得:![]() .
.
(1)观察发现
![]() _________;
_________;
![]() __________.
__________.
(2)初步应用
利用(1)的结论,解决下列问题:
①把![]() 拆成两个分子为1的正的真分数之差,即
拆成两个分子为1的正的真分数之差,即![]() __________;
__________;
②把![]() 拆成两个分子为1的正的真分数之和,即
拆成两个分子为1的正的真分数之和,即![]() __________.
__________.
(3)深入探究
定义“◆”是一种新的运算,若![]() ,
,![]() ,
,![]() ,则
,则![]() 计算的结果是_________.
计算的结果是_________.
(4)拓展延伸
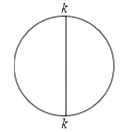
第一次用一条直径将圆周分成两个半圆(如图),在每个分点标上质数![]() ,记2个数的和为
,记2个数的和为![]() ,第二次将两个半圆都分成
,第二次将两个半圆都分成![]() 圆,在新产生的分点标相邻的已标的两个数的和的
圆,在新产生的分点标相邻的已标的两个数的和的![]() ,记4个数的和为
,记4个数的和为![]() ;第三次将四个
;第三次将四个![]() 圆分成
圆分成![]() 圆,在新产生的分点标相邻的已标的两个数的和的
圆,在新产生的分点标相邻的已标的两个数的和的![]() ,记8个数的和为
,记8个数的和为![]() ;第四次将八个
;第四次将八个![]() 圆分成
圆分成![]() 圆,在新产生的分点标相邻的已标的两个数的和的
圆,在新产生的分点标相邻的已标的两个数的和的![]() ,记16个数的和为
,记16个数的和为![]() ;……如此进行了
;……如此进行了![]() 次.
次.
①![]() _________(用含
_________(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
②![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
(1)求m的取值范围;
(2)是否存在实数m,使方程的两个实数根的倒数和等于0?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位计划购进![]() 三种型号的礼品共
三种型号的礼品共![]() 件,其中
件,其中![]() 型号礼品
型号礼品![]() 件,
件,![]() 型号礼品比
型号礼品比![]() 型号礼品多
型号礼品多![]() 件.已知三种型号礼品的单价如下表:
件.已知三种型号礼品的单价如下表:
型号 |
|
|
|
单价(元/件) |
|
|
|
(1)求计划购进![]() 和
和![]() 两种型号礼品分别多少件?
两种型号礼品分别多少件?
(2)实际购买时,厂家给予打折优惠销售(如: ![]() 折指原价
折指原价![]() ,在计划总价额不变的情况下,准备购进这批礼品.
,在计划总价额不变的情况下,准备购进这批礼品.
①若只购进![]() 两种型号礼品,且
两种型号礼品,且![]() 型礼品件数不超过
型礼品件数不超过![]() 型礼品的
型礼品的![]() 倍,求
倍,求![]() 型礼品最多购进多少件?
型礼品最多购进多少件?
②若只购进![]() 两种型号礼品,它们的单价分别打
两种型号礼品,它们的单价分别打![]() 折、
折、![]() 折,
折,![]() 均为整数,且购进的礼品总数比计划多
均为整数,且购进的礼品总数比计划多![]() 件,求
件,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电工想换房间的灯泡,已知灯泡到地面的距离为![]() ,现有一架家用可调节式脚踏人字梯,其中踏板、地面都是水平的.梯子的侧面简化结构如图所示,左右支撑架长度相等,
,现有一架家用可调节式脚踏人字梯,其中踏板、地面都是水平的.梯子的侧面简化结构如图所示,左右支撑架长度相等,![]() .设梯子一边
.设梯子一边![]() 与地面的夹角为
与地面的夹角为![]() ,且
,且![]() 可调节的范围为
可调节的范围为![]() .当
.当![]() 时,电工站在梯子安全挡中最高一档踏板
时,电工站在梯子安全挡中最高一档踏板![]() 上的最大触及高度为
上的最大触及高度为![]() .
.
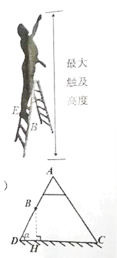
(1)当![]() 时,求踏板
时,求踏板![]() 离地面的高度
离地面的高度![]() .(精确到
.(精确到![]() )
)
(2)调节角度,试判断电工是否可以换下灯泡,并说明理由.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
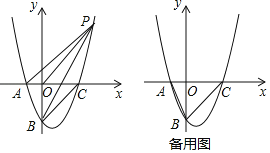
【题目】已知抛物线y=![]() x2+bx+c经过点A(﹣2,0),B(0、﹣4)与x轴交于另一点C,连接BC.
x2+bx+c经过点A(﹣2,0),B(0、﹣4)与x轴交于另一点C,连接BC.
(1)求抛物线的解析式;
(2)如图,P是第一象限内抛物线上一点,且S△PBO=S△PBC,求证:AP∥BC;
(3)在抛物线上是否存在点D,直线BD交x轴于点E,使△ABE与以A,B,C,E中的三点为顶点的三角形相似(不重合)?若存在,请求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=x+4的图象与反比例函数y2=![]() 的图象交于A(﹣1,a),B两点,与x轴交于点C.
的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求k.
(2)根据图象直接写出y1>y2时,x的取值范围.
(3)若反比例函数y2=![]() 与一次函数y1=x+4的图象总有交点,求k的取值.
与一次函数y1=x+4的图象总有交点,求k的取值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com