
ЁОЬтФПЁПФГЕЅЮЛМЦЛЎЙКНј![]() Ш§жжаЭКХЕФРёЦЗЙВ
Ш§жжаЭКХЕФРёЦЗЙВ![]() МўЃЌЦфжа
МўЃЌЦфжа![]() аЭКХРёЦЗ
аЭКХРёЦЗ![]() МўЃЌ
МўЃЌ![]() аЭКХРёЦЗБШ
аЭКХРёЦЗБШ![]() аЭКХРёЦЗЖр
аЭКХРёЦЗЖр![]() МўЃЎвбжЊШ§жжаЭКХРёЦЗЕФЕЅМлШчЯТБэЃК
МўЃЎвбжЊШ§жжаЭКХРёЦЗЕФЕЅМлШчЯТБэЃК
аЭКХ |
|
|
|
ЕЅМлЃЈдЊ/МўЃЉ |
|
|
|
ЃЈ1ЃЉЧѓМЦЛЎЙКНј![]() КЭ
КЭ![]() СНжжаЭКХРёЦЗЗжБ№ЖрЩйМў?
СНжжаЭКХРёЦЗЗжБ№ЖрЩйМў?
ЃЈ2ЃЉЪЕМЪЙКТђЪБЃЌГЇМвИјгшДђелгХЛнЯњЪлЃЈШчЃК ![]() елжИдМл
елжИдМл![]() ЃЌдкМЦЛЎзмМлЖюВЛБфЕФЧщПіЯТЃЌзМБИЙКНјетХњРёЦЗЃЎ
ЃЌдкМЦЛЎзмМлЖюВЛБфЕФЧщПіЯТЃЌзМБИЙКНјетХњРёЦЗЃЎ
ЂйШєжЛЙКНј![]() СНжжаЭКХРёЦЗЃЌЧв
СНжжаЭКХРёЦЗЃЌЧв![]() аЭРёЦЗМўЪ§ВЛГЌЙ§
аЭРёЦЗМўЪ§ВЛГЌЙ§![]() аЭРёЦЗЕФ
аЭРёЦЗЕФ![]() БЖЃЌЧѓ
БЖЃЌЧѓ![]() аЭРёЦЗзюЖрЙКНјЖрЩйМў?
аЭРёЦЗзюЖрЙКНјЖрЩйМў?
ЂкШєжЛЙКНј![]() СНжжаЭКХРёЦЗЃЌЫќУЧЕФЕЅМлЗжБ№Дђ
СНжжаЭКХРёЦЗЃЌЫќУЧЕФЕЅМлЗжБ№Дђ![]() елЁЂ
елЁЂ![]() елЃЌ
елЃЌ![]() ОљЮЊећЪ§ЃЌЧвЙКНјЕФРёЦЗзмЪ§БШМЦЛЎЖр
ОљЮЊећЪ§ЃЌЧвЙКНјЕФРёЦЗзмЪ§БШМЦЛЎЖр![]() МўЃЌЧѓ
МўЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉМЦЛЎЙКНјAКЭBаЭКХРёЦЗЗжБ№1200МўКЭ1000МўЃЛЃЈ2ЃЉЂйЙКНјBаЭКХРёЦЗзюЖр2440МўЃЛЂкa=7ЃЌb=8
ЁОНтЮіЁП
ЃЈ1ЃЉЩшМЦЛЎBаЭРёЦЗ![]() МўЃЌAаЭРёЦЗ
МўЃЌAаЭРёЦЗ![]() МўЃЌИљОнзмЪ§ЮЊ2700МўСаЗНГЬЧѓНтМДПЩЃЛ
МўЃЌИљОнзмЪ§ЮЊ2700МўСаЗНГЬЧѓНтМДПЩЃЛ
ЃЈ2ЃЉЯШЧѓЕУМЦЛЎзмМлЖюЃЌЂйЩшЙКНјBаЭРёЦЗmМўЃЌCаЭРёЦЗnМўЃЌИљОнзмМлЖюМА![]() аЭРёЦЗМўЪ§ВЛГЌЙ§
аЭРёЦЗМўЪ§ВЛГЌЙ§![]() аЭРёЦЗЕФ
аЭРёЦЗЕФ![]() БЖЃЌСаЪНМЦЫуМДПЩЃЛ
БЖЃЌСаЪНМЦЫуМДПЩЃЛ
ЂкЙКНјAаЭРёЦЗpМўЃЌBаЭРёЦЗqМўЃЌИљОнЬтвтЕУ![]() ЃЌИљОнЬтвт
ЃЌИљОнЬтвт![]() ЃЌ
ЃЌ![]() ЃЌећРэЕУ
ЃЌећРэЕУ![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌдйИљОн
ЃЌдйИљОн![]() ЁЂ
ЁЂ![]() ЮЊаЁгк9ЕФећЪ§ЃЌМДПЩЧѓНтЃЎ
ЮЊаЁгк9ЕФећЪ§ЃЌМДПЩЧѓНтЃЎ
ЃЈ1ЃЉЩшМЦЛЎBаЭРёЦЗ![]() МўЃЌAаЭРёЦЗ
МўЃЌAаЭРёЦЗ![]() МўЃЌгЩЬтвтЕУЃК
МўЃЌгЩЬтвтЕУЃК
![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
дђ![]() ЃЌ
ЃЌ
Д№ЃКМЦЛЎЙКНјAКЭBаЭКХРёЦЗЗжБ№1200МўКЭ1000МўЃЛ
ЃЈ2ЃЉМЦЛЎзмМлЮЊЃК![]() (дЊ)ЃЌ
(дЊ)ЃЌ
ЂйЙКНјBаЭРёЦЗ![]() МўЃЌCаЭРёЦЗ
МўЃЌCаЭРёЦЗ![]() МўЃЌгЩЬтвтЕУЃК
МўЃЌгЩЬтвтЕУЃК
![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
Д№ЃКЙКНјBаЭКХРёЦЗзюЖр2440МўЃЛ
ЂкЙКНјAаЭРёЦЗ![]() МўЃЌBаЭРёЦЗ
МўЃЌBаЭРёЦЗ![]() МўЃЌгЩЬтвтЕУЃК
МўЃЌгЩЬтвтЕУЃК
![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌ
ЃЌ
Ђй ![]() ЃЌ
ЃЌ![]() ЃЌЕУ
ЃЌЕУ![]() ЃЛ
ЃЛ
Ђк![]() ЃЌ
ЃЌ![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌВЛКЯЬтвтЃЛ
ЃЌВЛКЯЬтвтЃЛ
Ђл![]() ЃЌ
ЃЌ![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌВЛКЯЬтвтЃЛ
ЃЌВЛКЯЬтвтЃЛ
злЩЯЫљЪіЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ


 СњШЫЭМЪщПьРжМйЦкЪюМйзївЕжЃжнДѓбЇГіАцЩчЯЕСаД№АИ
СњШЫЭМЪщПьРжМйЦкЪюМйзївЕжЃжнДѓбЇГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCЪЧЁбOЕФФкНгШ§НЧаЮЃЎAEЪЧЁбOЕФжБОЖЃЌНЛBCгкЕуGЃЎЙ§ЕуAзїAFЁЭBCЃЌAFЗжБ№гыBCЁЂЁбOНЛгкЕуDЁЂFЃЌСЌНгBEЁЂCFЃЎ
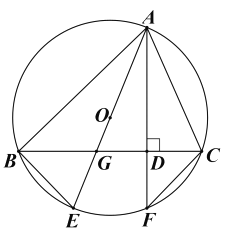
ЃЈ1ЃЉЧѓжЄЃКЁЯBAEЃНЁЯCAFЃЛ
ЃЈ2ЃЉШєABЃН8ЃЌACЃН6ЃЌAGЃН5ЃЌЧѓAFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮ![]() жаЃЌ
жаЃЌ![]() ЪЧЖдНЧЯп
ЪЧЖдНЧЯп![]() ЩЯЕФвЛИіЖЏЕу
ЩЯЕФвЛИіЖЏЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШчЭМЂйЃЌЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌСЌНг![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЕФбгГЄЯпНЛБп
ЕФбгГЄЯпНЛБп![]() гкЕу
гкЕу![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() КЭ
КЭ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ3ЃЉШчЭМЂлЃЌЙ§Еу![]() зї
зї![]() гк
гк![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФУцЛ§ЃЎ
ЕФУцЛ§ЃЎ
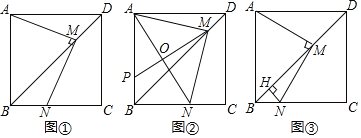
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌФГжабЇЪ§бЇЛюЖЏаЁзщдкбЇЯАСЫЁАРћгУШ§НЧКЏЪ§ВтИпЁБКѓЃЌбЁЖЈВтСПаЁКгЖдАЖвЛДБНЈжўЮяBCЕФИпЖШЃЌЫћУЧЯШдкаБЦТЩЯЕФDДІЃЌВтЕУНЈжўЮяЖЅЖЫBЕФбіНЧЮЊ30ЁуЃЎЧвDРыЕиУцЕФИпЖШDE=5mЃЎЦТЕзEA=30mЃЌШЛКѓдкAДІВтЕУНЈжўЮяЖЅЖЫBЕФбіНЧЪЧ60ЁуЃЌЕуEЃЌAЃЌCдкЭЌвЛЫЎЦНЯпЩЯЃЌЧѓНЈжўЮяBCЕФИпЃЎЃЈНсЙћгУКЌгаИљКХЕФЪНзгБэЪОЃЉ
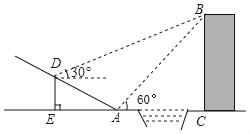
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгЩЫФИіе§ЗНаЮЯрПђЦДГЩЕФееЦЌЧНШчЭМЫљЪОЃЌвбжЊе§ЗНаЮ![]() ЃЌе§ЗНаЮ
ЃЌе§ЗНаЮ![]() ЃЌе§ЗНаЮ
ЃЌе§ЗНаЮ![]() ЕФЃЎУцЛ§ЗжБ№ЮЊ
ЕФЃЎУцЛ§ЗжБ№ЮЊ![]() ЦНЗНЗжУзЃЌ
ЦНЗНЗжУзЃЌ![]() ЦНЗНЗжУзЃЌ
ЦНЗНЗжУзЃЌ![]() ЦНЗНЗжУзЃЌдђе§ЗНаЮ
ЦНЗНЗжУзЃЌдђе§ЗНаЮ![]() ЕФУцЛ§ЮЊ__________ЦНЗНЗжУзЃЎ
ЕФУцЛ§ЮЊ__________ЦНЗНЗжУзЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕу![]() дкЗДБШР§КЏЪ§
дкЗДБШР§КЏЪ§![]() ЕФЭМЯѓЩЯЃЌЕу
ЕФЭМЯѓЩЯЃЌЕу![]() дкЗДБШР§КЏЪ§
дкЗДБШР§КЏЪ§![]() ЕФЭМЯѓЩЯЃЌЧв
ЕФЭМЯѓЩЯЃЌЧв![]() ЃЌЯпЖЮ
ЃЌЯпЖЮ![]() НЛЗДБШР§КЏЪ§
НЛЗДБШР§КЏЪ§![]() ЕФЭМЯѓгкСэвЛЕу
ЕФЭМЯѓгкСэвЛЕу![]() ЃЌСЌНс
ЃЌСЌНс![]() ЃЎШєЕу
ЃЎШєЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЕФжЕЮЊ_________ЃЎ
ЕФжЕЮЊ_________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
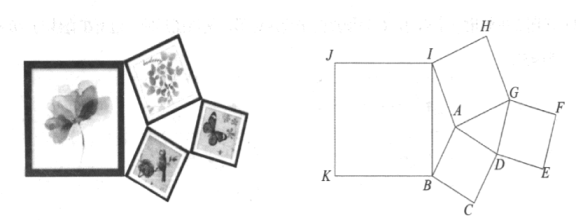
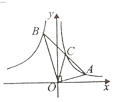
ЁОЬтФПЁПаЁУїбЇЯАЭъЁЖЯрЫЦШ§НЧаЮЁЗвЛеТКѓЃЌЗЂЯжСЫвЛИігаШЄЕФНсТлЃКдкСНИіВЛЯрЫЦЕФжБНЧШ§НЧаЮжаЃЌЗжБ№ДцдкОЙ§жБНЧЖЅЕуЕФвЛЬѕжБЯпЃЌАбжБНЧШ§НЧаЮЗжГЩСНИіаЁШ§НЧаЮКѓЃЌШчЙћЕквЛИіжБНЧШ§НЧаЮЗжИюГіРДЕФвЛИіаЁШ§НЧаЮгыЕкЖўИіжБНЧШ§НЧаЮЗжИюГіРДЕФвЛИіаЁШ§НЧаЮЯрЫЦЃЌФЧУДЗжИюГіРДЕФСэЭтСНИіаЁШ§НЧаЮвВЯрЫЦЃЎЫћАбетбљЕФСНЬѕжБЯпГЦЮЊетСНИіжБНЧШ§НЧаЮЕФЯрЫЦЗжИюЯпЃЎШчЭМ1ЁЂЭМ2ЃЌжБЯпCGЁЂDHЗжБ№ЪЧСНИіВЛЯрЫЦЕФRtЁїABCКЭRtЁїDEFЕФЯрЫЦЗжИюЯпЃЌCGЁЂDHЗжБ№гыаББпABЁЂEFНЛгкЕуGЁЂHЃЌШчЙћЁїBCGгыЁїDFHЯрЫЦЃЌACЃН3ЃЌABЃН5ЃЌDEЃН4ЃЌDFЃН8ЃЌФЧУДAGЃН_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
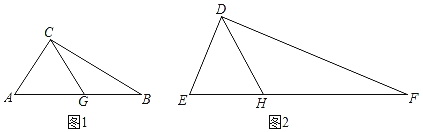
ЁОЬтФПЁПвбжЊШ§НЧаЮABCЃЌADЮЊBCБпжаЯпЃЌPЮЊBCЩЯвЛЖЏЕуЃЌЙ§ЕуPзїADЕФЦНааЯпЃЌНЛжБЯпABЛђбгГЄЯпгкЕуQЃЌНЛCAЛђбгГЄЯпгкЕуRЃЎ
ЃЈ1ЃЉЕБЕуPдкBDЩЯдЫЖЏЪБЃЌЙ§ЕуQзїBCЕФЦНааЯпНЛADгкEЕуЃЌНЛACгкFЕуЃЌЧѓжЄЃКQEЃНEFЃЛ
ЃЈ2ЃЉЕБЕуPдкBCЩЯдЫЖЏЪБЃЌЧѓжЄЃКPQ+PRЮЊЖЈжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
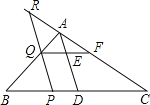
ЁОЬтФПЁПШчЭМЃЌвбжЊЖўДЮКЏЪ§yЃНx2Љ2x+mЕФЭМЯѓгыxжсНЛгкЕуAЁЂBЃЌгыyжсНЛгкЕуCЃЌжБЯпACНЛЖўДЮКЏЪ§ЭМЯѓЕФЖдГЦжсгкЕуDЃЌШєЕуCЮЊADЕФжаЕуЃЎ
ЃЈ1ЃЉЧѓmЕФжЕЃЛ
ЃЈ2ЃЉШєЖўДЮКЏЪ§ЭМЯѓЩЯгавЛЕуQЃЌЪЙЕУtanЁЯABQЃН3ЃЌЧѓЕуQЕФзјБъЃЛ
ЃЈ3ЃЉЖдгкЃЈ2ЃЉжаЕФQЕуЃЌдкЖўДЮКЏЪ§ЭМЯѓЩЯЪЧЗёДцдкЕуPЃЌЪЙЕУЁїQBPЁзЁїCOAЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com