
【题目】如图,△ABC是⊙O的内接三角形.AE是⊙O的直径,交BC于点G.过点A作AF⊥BC,AF分别与BC、⊙O交于点D、F,连接BE、CF.
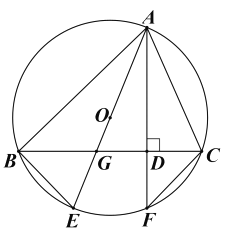
(1)求证:∠BAE=∠CAF;
(2)若AB=8,AC=6,AG=5,求AF的长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)由圆周角定理得出∠ABE=90°,得出∠BAE+∠BEA=90°,由AF⊥BC得出∠ACD+∠CAF =90°,由圆周角定理得出∠BEA=∠ACD,即可得出结论;
(2)先证明∠ABC=∠AFC,∠BAE=∠CAF得△ABG∽△AFC,得到![]() 即可得到答案.
即可得到答案.
解(1)∵AE是⊙O的直径,
∴∠ABE=90°,
∴∠BAE+∠BEA=90°,
∵AF⊥BC,
∴∠ADC=90°,
∴∠ACD+∠CAF =90°,
又∵∠BEA=∠ACD,
∴∠BAE=∠CAF;
(2)∵∠ABC与∠AFC是![]() 的圆周角
的圆周角
∴∠ABC=∠AFC
∵∠BAE=∠CAF
∴△ABG∽△AFC
∴![]()
∵AB=8,AC=6,AG=5
∴![]() 得
得![]()


 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:是长方形纸片ABCD折叠的情况,纸片的宽度AB=8cm,长AD=10cm,AD沿点A对折,点D正好落在BC上的M处,AE是折痕.
(1)求CM的长;
(2)求梯形ABCE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在游乐场坐过山车,某一分钟内过山车高度h(米)与时间t(秒)之间的函数图象如图所示.请结合图象回答:
(1)①当t=41秒时,h的值是多少?并说明它的实际意义;
②过山车所达到的最大高度是多少?
(2)请描述30秒后,高度h(米)随时间t(秒)的变化情况.

查看答案和解析>>
科目:初中数学 来源: 题型:
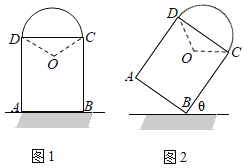
【题目】图1为一艺术拱门,下部为矩形ABCD,AB、AD的长分别为![]() m和4m,上部是圆心为O的劣弧CD,∠COD=120°.现欲以点B为支点将拱门放倒,放倒过程中矩形ABCD所在的平面始终与地面垂直,如图2所示.设BC与地面水平线所成的角为
m和4m,上部是圆心为O的劣弧CD,∠COD=120°.现欲以点B为支点将拱门放倒,放倒过程中矩形ABCD所在的平面始终与地面垂直,如图2所示.设BC与地面水平线所成的角为![]() ,记拱门上的点到地面的距离为h,当h取最大值时,此时
,记拱门上的点到地面的距离为h,当h取最大值时,此时![]() 为________°.
为________°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果三角形的两个内角∠α与∠β满足∠α=2∠β,那么,我们将这样的三角形称为“倍角三角形”.如果一个等腰三角形是“倍角三角形”,那么这个等腰三角形的腰长与底边长的比值为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一拱桥的桥拱是圆弧形,已知桥拱的水面跨度AB(弧所对的弦的长)为8米,拱高CD(弧的中点到弦的距离)为2米.
(1)求桥拱所在圆的半径长;
(2)如果水面AB上升到EF时,从点E测得桥顶D的仰角为α,且cotα=3,求水面上升的高度.
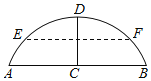
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中(如图),已知函数
中(如图),已知函数![]() 的图像和反比例函数的在第一象限交于A点,其中点A的横坐标是1.
的图像和反比例函数的在第一象限交于A点,其中点A的横坐标是1.
(1)求反比例函数的解析式;
(2)把直线![]() 平移后与
平移后与![]() 轴相交于点B,且
轴相交于点B,且![]() ,求平移后直线的解析式.
,求平移后直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位计划购进![]() 三种型号的礼品共
三种型号的礼品共![]() 件,其中
件,其中![]() 型号礼品
型号礼品![]() 件,
件,![]() 型号礼品比
型号礼品比![]() 型号礼品多
型号礼品多![]() 件.已知三种型号礼品的单价如下表:
件.已知三种型号礼品的单价如下表:
型号 |
|
|
|
单价(元/件) |
|
|
|
(1)求计划购进![]() 和
和![]() 两种型号礼品分别多少件?
两种型号礼品分别多少件?
(2)实际购买时,厂家给予打折优惠销售(如: ![]() 折指原价
折指原价![]() ,在计划总价额不变的情况下,准备购进这批礼品.
,在计划总价额不变的情况下,准备购进这批礼品.
①若只购进![]() 两种型号礼品,且
两种型号礼品,且![]() 型礼品件数不超过
型礼品件数不超过![]() 型礼品的
型礼品的![]() 倍,求
倍,求![]() 型礼品最多购进多少件?
型礼品最多购进多少件?
②若只购进![]() 两种型号礼品,它们的单价分别打
两种型号礼品,它们的单价分别打![]() 折、
折、![]() 折,
折,![]() 均为整数,且购进的礼品总数比计划多
均为整数,且购进的礼品总数比计划多![]() 件,求
件,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com