
【题目】在平面直角坐标系![]() 中(如图),已知函数
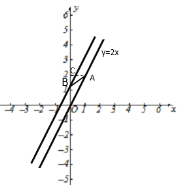
中(如图),已知函数![]() 的图像和反比例函数的在第一象限交于A点,其中点A的横坐标是1.
的图像和反比例函数的在第一象限交于A点,其中点A的横坐标是1.
(1)求反比例函数的解析式;
(2)把直线![]() 平移后与
平移后与![]() 轴相交于点B,且
轴相交于点B,且![]() ,求平移后直线的解析式.
,求平移后直线的解析式.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)将点A的横坐标代入y=2x中,得到点A的纵坐标,设反比例函数解析式为![]() ,再将点A的坐标代入解答;
,再将点A的坐标代入解答;
(2)过点A作AC⊥y轴于C,则AC=1,OC=2,根据AB=OB,得到直线y=2x向上平移,设平移后的直线解析式为![]() +b,则OB=b,根据勾股定理得到
+b,则OB=b,根据勾股定理得到![]() ,求出
,求出![]() ,即可得到函数解析式.
,即可得到函数解析式.
(1)将点A的横坐标1代入y=2x中,得y=2,
∴点A的坐标为(1,2),
设反比例函数解析式为![]() ,将点A的坐标代入,得到k=2,
,将点A的坐标代入,得到k=2,
∴反比例函数解析式为![]() ;
;
(2)过点A作AC⊥y轴于C,则AC=1,OC=2,
∵AB=OB,
∴直线y=2x向上平移,
设平移后的直线解析式为![]() +b,则OB=b,
+b,则OB=b,
∵![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴平移后的解析式为:![]() .
.


科目:初中数学 来源: 题型:
【题目】近几年,随着电子产品的广泛应用,学生的近视发生率出现低龄化趋势,引起了相关部门的重视.某区为了了解在校学生的近视低龄化情况,对本区7-18岁在校近视学生进行了简单的随机抽样调查,并绘制了以下两幅不完整的统计图.

请根据图中信息,回答下列问题:
(1)这次抽样调查中共调查了近视学生 人;
(2)请补全条形统计图;
(3)扇形统计图中10-12岁部分的圆心角的度数是 ;
(4)据统计,该区7-18岁在校学生近视人数约为10万,请估计其中7-12岁的近视学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
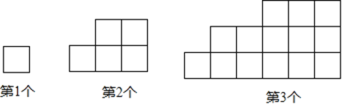
【题目】下列图形都是由大小相同的小正方形按一定规律组成的,其中第1个图形的周长为4,第2个图形的周长为10,第3个图形的周长为18,…,按此规律排列,回答下列问题:
(1)第5个图形的周长为 ;
(2)第![]() 个图形的周长为 ;
个图形的周长为 ;
(3)若第![]() 个图形的周长为180,则
个图形的周长为180,则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
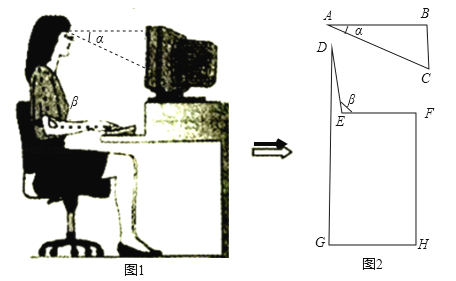
【题目】(2017江西省)如图1,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”α约为20°,而当手指接触键盘时,肘部形成的“手肘角”β约为100°.图2是其侧面简化示意图,其中视线AB水平,且与屏幕BC垂直.
(1)若屏幕上下宽BC=20cm,科学使用电脑时,求眼睛与屏幕的最短距离AB的长;
(2)若肩膀到水平地面的距离DG=100cm,上臂DE=30cm,下臂EF水平放置在键盘上,其到地面的距离FH=72cm.请判断此时β是否符合科学要求的100°?
(参考数据:sin69°≈![]() ,cos21°≈
,cos21°≈![]() ,tan20°≈
,tan20°≈![]() ,tan43°≈
,tan43°≈![]() ,所有结果精确到个位)
,所有结果精确到个位)
查看答案和解析>>
科目:初中数学 来源: 题型:
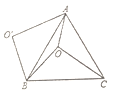
【题目】如图,O是等边![]() 内一点,
内一点,![]() ,以点B为旋转中心,将线段BO逆时针旋转
,以点B为旋转中心,将线段BO逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,则下列结论:
,则下列结论:
①![]() 可以由
可以由![]() 绕点B逆时针旋转
绕点B逆时针旋转![]() 得到
得到
②连接![]() ,则
,则![]()
③![]()
④![]()
其中正确的结论是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
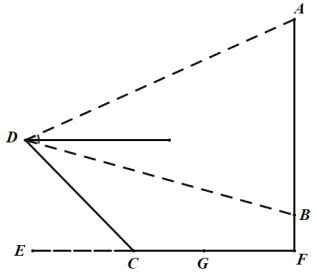
【题目】如图,为测量瀑布![]() 的高度,测量人员在瀑布对面山上的
的高度,测量人员在瀑布对面山上的![]() 点处测得瀑布顶端
点处测得瀑布顶端![]() 点的仰角是
点的仰角是![]() ,测得瀑布底端
,测得瀑布底端![]() 点的俯角是
点的俯角是![]() ,
,![]() 与水平面垂直.又在瀑布下的水平面测得
与水平面垂直.又在瀑布下的水平面测得![]() ,
,![]() (注:
(注:![]() 、
、![]() 、
、![]() 三点在同一直线上,
三点在同一直线上,![]() 于点
于点![]() ),斜坡
),斜坡![]() ,坡角
,坡角![]() ,那么瀑布
,那么瀑布![]() 的高度约为( ).(精确到
的高度约为( ).(精确到![]() ,参考数据:
,参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
A.![]()
![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假旅游旺季即将到来,外出旅游的人数不断攀升,去海边游玩是大多数人不错的选择,去海边游玩的人都会选择自己购买海产品进行加工,某商家7月1日进购了一批扇贝与爬爬虾共计200千克,已知扇贝进价10元/千克,售价30元/千克,爬爬虾进价20元/千克,售价30元/千克.
(1)若这批海产品全部售完获利不低于3000元,则扇贝至少进购多少千克?
(2)第一批扇贝和爬爬虾很快售完,于是商家决定购进第二批扇贝与爬爬虾,两种海产品的进价不变,扇贝售价比第一批上涨![]() ,爬爬虾售价比第一批上涨
,爬爬虾售价比第一批上涨![]() ,销量与(1)中获得最低利润时的销量相比,扇贝的销量下降了
,销量与(1)中获得最低利润时的销量相比,扇贝的销量下降了![]() ,爬爬虾的销量不变,结果第二批已经卖掉的扇贝与爬爬虾的销售总额比(1)中第一批扇贝与爬爬虾售完后对应的最低销售总额增加了
,爬爬虾的销量不变,结果第二批已经卖掉的扇贝与爬爬虾的销售总额比(1)中第一批扇贝与爬爬虾售完后对应的最低销售总额增加了![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
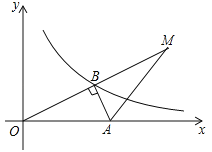
【题目】如图,在平面直角坐标系中,Rt△AOB的斜边OA在x轴的正半轴上,∠OBA=90°,且tan∠AOB=![]() ,OB=
,OB=![]() ,反比例函数
,反比例函数![]() 的图象经过点B.
的图象经过点B.
(1)求反比例函数的表达式;
(2)若△AMB与△AOB关于直线AB对称,一次函数y=mx+n的图象过点M、A,求一次函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
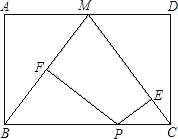
【题目】如图,点M是矩形ABCD的边AD的中点,点P是BC边上一动点,PE⊥MC,PF⊥BM,垂足为E、F.
(1)当矩形ABCD的长与宽满足什么条件时,四边形PEMF为矩形?猜想并证明你的结论.
(2)在(1)中,当点P运动到什么位置时,矩形PEMF变为正方形,为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com