
ЁОЬтФПЁПЪюМйТУгЮЭњМОМДНЋЕНРДЃЌЭтГіТУгЮЕФШЫЪ§ВЛЖЯХЪЩ§ЃЌШЅКЃБпгЮЭцЪЧДѓЖрЪ§ШЫВЛДэЕФбЁдёЃЌШЅКЃБпгЮЭцЕФШЫЖМЛсбЁдёздМКЙКТђКЃВњЦЗНјааМгЙЄЃЌФГЩЬМв7дТ1ШеНјЙКСЫвЛХњЩШБДгыХРХРЯКЙВМЦ200ЧЇПЫЃЌвбжЊЩШБДНјМл10дЊ/ЧЇПЫЃЌЪлМл30дЊ/ЧЇПЫЃЌХРХРЯКНјМл20дЊ/ЧЇПЫЃЌЪлМл30дЊ/ЧЇПЫЃЎ
ЃЈ1ЃЉШєетХњКЃВњЦЗШЋВПЪлЭъЛёРћВЛЕЭгк3000дЊЃЌдђЩШБДжСЩйНјЙКЖрЩйЧЇПЫЃП
ЃЈ2ЃЉЕквЛХњЩШБДКЭХРХРЯККмПьЪлЭъЃЌгкЪЧЩЬМвОіЖЈЙКНјЕкЖўХњЩШБДгыХРХРЯКЃЌСНжжКЃВњЦЗЕФНјМлВЛБфЃЌЩШБДЪлМлБШЕквЛХњЩЯеЧ![]() ЃЌХРХРЯКЪлМлБШЕквЛХњЩЯеЧ
ЃЌХРХРЯКЪлМлБШЕквЛХњЩЯеЧ![]() ЃЌЯњСПгыЃЈ1ЃЉжаЛёЕУзюЕЭРћШѓЪБЕФЯњСПЯрБШЃЌЩШБДЕФЯњСПЯТНЕСЫ
ЃЌЯњСПгыЃЈ1ЃЉжаЛёЕУзюЕЭРћШѓЪБЕФЯњСПЯрБШЃЌЩШБДЕФЯњСПЯТНЕСЫ![]() ЃЌХРХРЯКЕФЯњСПВЛБфЃЌНсЙћЕкЖўХњвбОТєЕєЕФЩШБДгыХРХРЯКЕФЯњЪлзмЖюБШЃЈ1ЃЉжаЕквЛХњЩШБДгыХРХРЯКЪлЭъКѓЖдгІЕФзюЕЭЯњЪлзмЖюдіМгСЫ
ЃЌХРХРЯКЕФЯњСПВЛБфЃЌНсЙћЕкЖўХњвбОТєЕєЕФЩШБДгыХРХРЯКЕФЯњЪлзмЖюБШЃЈ1ЃЉжаЕквЛХњЩШБДгыХРХРЯКЪлЭъКѓЖдгІЕФзюЕЭЯњЪлзмЖюдіМгСЫ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉЩШБДжСЩйНјЙК100ЧЇПЫЃЛЃЈ2ЃЉ![]() ЕФжЕЮЊ25ЃЎ
ЕФжЕЮЊ25ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЩшНјЙКЩШБДxЧЇПЫЃЌдђНјЙКХРХРЯКЃЈ200ЃxЃЉЧЇПЫЃЌИљОнЛёРћВЛЕЭгк3000дЊСаВЛЕШЪНЧѓНтМДПЩЃЛ
ЃЈ2ЃЉИљОнЯњЪлЖюЃНЪлМлЁСЯњСПЃЌНсКЯЕкЖўХњвбОТєЕєЕФЩШБДгыХРХРЯКЕФЯњЪлзмЖюБШЃЈ1ЃЉжаЕквЛХњЩШБДгыХРХРЯКЪлЭъКѓЖдгІЕФзюЕЭЯњЪлзмЖюдіМгСЫ![]() СаГіЗНГЬЃЌећРэКѓНтЗНГЬМДПЩЕУЕНaЕФжЕЃЎ
СаГіЗНГЬЃЌећРэКѓНтЗНГЬМДПЩЕУЕНaЕФжЕЃЎ
НтЃКЃЈ1ЃЉЩшНјЙКЩШБДxЧЇПЫЃЌдђНјЙКХРХРЯКЃЈ200ЃxЃЉЧЇПЫЃЌ
гЩЬтвтЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
Д№ЃКЩШБДжСЩйНјЙК100ЧЇПЫЃЛ
ЃЈ2ЃЉЕБЃЈ1ЃЉжаЛёЕУзюЕЭРћШѓЪБЃЌЩШБДЕФЯњСПЮЊ100ЧЇПЫЃЌХРХРЯКЕФЯњСПвВЪЧ100ЧЇПЫЃЌ
гЩЬтвтЕУЃК![]() ЃЌ
ЃЌ
ећРэЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК![]() Лђ
Лђ![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ
Д№ЃК![]() ЕФжЕЮЊ25ЃЎ
ЕФжЕЮЊ25ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТУцЕФВФСЯЃК
ШчЙћКЏЪ§![]() ТњзуЃКЖдгкздБфСП
ТњзуЃКЖдгкздБфСП![]() ЕФШЁжЕЗЖЮЇФкЕФШЮвт
ЕФШЁжЕЗЖЮЇФкЕФШЮвт![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЃЈ1ЃЉШє![]() ЃЌЖМга
ЃЌЖМга![]() ЃЌдђГЦ
ЃЌдђГЦ![]() ЪЧдіКЏЪ§ЃЛ
ЪЧдіКЏЪ§ЃЛ
ЃЈ2ЃЉШє![]() ЃЌЖМга
ЃЌЖМга![]() ЃЌдђГЦ
ЃЌдђГЦ![]() ЪЧМѕКЏЪ§ЃЎ
ЪЧМѕКЏЪ§ЃЎ
Р§ЬтЃКжЄУїКЏЪ§![]() ЪЧМѕКЏЪ§ЃЎ
ЪЧМѕКЏЪ§ЃЎ
жЄУїЃКЩш![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ
Ёп![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ![]() ЃЎЁр
ЃЎЁр![]() ЃЎМД
ЃЎМД![]() ЃЎ
ЃЎ
Ёр![]() ЃЎЁрКЏЪ§
ЃЎЁрКЏЪ§![]() ЃЈ
ЃЈ![]() ЃЉЪЧМѕКЏЪ§ЃЎ
ЃЉЪЧМѕКЏЪ§ЃЎ
ИљОнвдЩЯВФСЯЃЌНтД№ЯТУцЕФЮЪЬтЃК
МКжЊКЏЪ§![]() ЃЈ
ЃЈ![]() ЃЉЃЌ
ЃЉЃЌ
ЃЈ1ЃЉМЦЫуЃК![]() _______ЃЌ
_______ЃЌ![]() _______ЃЛ
_______ЃЛ
ЃЈ2ЃЉВТЯыЃККЏЪ§![]() ЃЈ
ЃЈ![]() ЃЉЪЧ_______КЏЪ§ЃЈЬюЁАдіЁБЛђЁАМѕЁБЃЉЃЛ
ЃЉЪЧ_______КЏЪ§ЃЈЬюЁАдіЁБЛђЁАМѕЁБЃЉЃЛ
ЃЈ3ЃЉЧыЗТееР§ЬтжЄУїФуЕФВТЯыЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
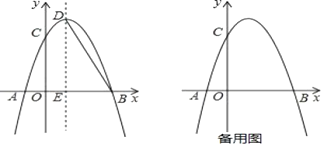
ЁОЬтФПЁПХзЮяЯпyЃНx2+bx+cЕФЭМЯѓОЙ§ЕуA(Љ1ЃЌ0)ЃЌB(0ЃЌЉ3)ЃЎ
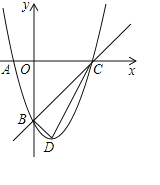
ЃЈ1ЃЉЧѓетИіХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉХзЮяЯпгыxжсЕФСэвЛНЛЕуЮЊCЃЌХзЮяЯпЕФЖЅЕуЮЊDЃЌХаЖЯЁїCBDЕФаЮзДЃЛ
ЃЈ3ЃЉжБЯпBNЁЮxжсЃЌНЛХзЮяЯпгкСэвЛЕуNЃЌЕуPЪЧжБЯпBNЯТЗНЕФХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЈЕуPВЛгыЕуBКЭЕуNжиКЯЃЉЃЌЙ§ЕуPзїxжсЕФДЙЯпЃЌНЛжБЯпBCгкЕуQЃЌЕБЫФБпаЮBPNQЕФУцЛ§зюДѓЪБЃЌЧѓГіЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЈШчЭМЃЉЃЌвбжЊКЏЪ§
жаЃЈШчЭМЃЉЃЌвбжЊКЏЪ§![]() ЕФЭМЯёКЭЗДБШР§КЏЪ§ЕФдкЕквЛЯѓЯоНЛгкAЕуЃЌЦфжаЕуAЕФКсзјБъЪЧ1ЃЎ
ЕФЭМЯёКЭЗДБШР§КЏЪ§ЕФдкЕквЛЯѓЯоНЛгкAЕуЃЌЦфжаЕуAЕФКсзјБъЪЧ1ЃЎ
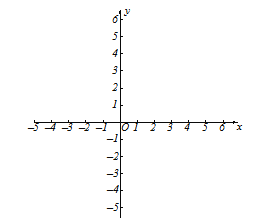
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉАбжБЯп![]() ЦНвЦКѓгы
ЦНвЦКѓгы![]() жсЯрНЛгкЕуBЃЌЧв
жсЯрНЛгкЕуBЃЌЧв![]() ЃЌЧѓЦНвЦКѓжБЯпЕФНтЮіЪНЃЎ
ЃЌЧѓЦНвЦКѓжБЯпЕФНтЮіЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮ![]() жаЃЌСЌНг
жаЃЌСЌНг![]() ЃЌвдЕу
ЃЌвдЕу![]() ЮЊдВаФЃЌ
ЮЊдВаФЃЌ![]() ЮЊАыОЖЛЛЁЃЌНЛ
ЮЊАыОЖЛЛЁЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌвбжЊ
ЃЌвбжЊ![]() ЃЌ
ЃЌ![]() ЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЮЊ_______ЃЎЃЈНсЙћБЃСє
ЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЮЊ_______ЃЎЃЈНсЙћБЃСє![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
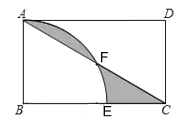
ЁОЬтФПЁПШчЭМЫљЪОЕФЧњБпШ§НЧаЮПЩАДЯТЪіЗНЗЈзїГіЃКзїЕШБпШ§НЧаЮ![]() ЃЛЗжБ№вдЕу
ЃЛЗжБ№вдЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊдВаФЃЌвд
ЮЊдВаФЃЌвд![]() ЕФГЄЮЊАыОЖзї
ЕФГЄЮЊАыОЖзї![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎШ§ЖЮЛЁЫљЮЇГЩЕФЭМаЮОЭЪЧвЛИіЧњБпШ§НЧаЮЃЌШчЙћвЛИіЧњБпШ§НЧаЮЕФжмГЄЮЊ
ЃЎШ§ЖЮЛЁЫљЮЇГЩЕФЭМаЮОЭЪЧвЛИіЧњБпШ§НЧаЮЃЌШчЙћвЛИіЧњБпШ§НЧаЮЕФжмГЄЮЊ![]() ЃЌФЧУДетИіЧњБпШ§НЧаЮЕФУцЛ§ЪЧ___________ЃЎ
ЃЌФЧУДетИіЧњБпШ§НЧаЮЕФУцЛ§ЪЧ___________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() КЭЕу
КЭЕу![]() ЃЌгы
ЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌЕу
ЃЌЕу![]() зјБъЮЊ
зјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() зјБъЮЊ
зјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЪЧХзЮяЯпЕФЖЅЕуЃЌЙ§Еу
ЪЧХзЮяЯпЕФЖЅЕуЃЌЙ§Еу![]() зї
зї![]() жсЕФДЙЯпЃЌДЙзуЮЊ
жсЕФДЙЯпЃЌДЙзуЮЊ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНМАЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ2ЃЉЕу![]() ЪЧХзЮяЯпЩЯЕФЖЏЕуЃЌЕБ
ЪЧХзЮяЯпЩЯЕФЖЏЕуЃЌЕБ![]() ЪБЃЌЧѓЕу
ЪБЃЌЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉШєЕу![]() ЪЧ
ЪЧ![]() жсЩЯЗНХзЮяЯпЩЯЕФЖЏЕуЃЌвд
жсЩЯЗНХзЮяЯпЩЯЕФЖЏЕуЃЌвд![]() ЮЊБпзїе§ЗНаЮ
ЮЊБпзїе§ЗНаЮ![]() ЃЌЫцзХЕу
ЃЌЫцзХЕу![]() ЕФдЫЖЏЃЌе§ЗНаЮЕФДѓаЁЁЂЮЛжУвВЫцзХИФБфЃЌЕБЖЅЕу
ЕФдЫЖЏЃЌе§ЗНаЮЕФДѓаЁЁЂЮЛжУвВЫцзХИФБфЃЌЕБЖЅЕу![]() Лђ
Лђ![]() ЧЁКУТфдк
ЧЁКУТфдк![]() жсЩЯЪБЃЌЧыжБНгаДГіЕу
жсЩЯЪБЃЌЧыжБНгаДГіЕу![]() ЕФКсзјБъЃЎ
ЕФКсзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдкОиаЮABCDжаЃЌЖЏЕуEДгAГіЗЂЃЌбиAЁњBЁњCЗНЯђдЫЖЏЃЌЕБЕуEЕНДяЕуCЪБЭЃжЙдЫЖЏЃЌЙ§ЕуEзїEFЁЭAEНЛCDгкЕуFЃЌЩшЕуEдЫЖЏТЗГЬЮЊxЃЌCF=yЃЌШчЭМ2ЫљБэЪОЕФЪЧyгыxЕФКЏЪ§ЙиЯЕЕФДѓжТЭМЯѓЃЌИјГіЯТСаНсТлЃКЂйa=3ЃЛЂкЕБCF=![]() ЪБЃЌЕуEЕФдЫЖЏТЗГЬЮЊ
ЪБЃЌЕуEЕФдЫЖЏТЗГЬЮЊ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЌдђЯТСаХаЖЯе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
ЃЌдђЯТСаХаЖЯе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
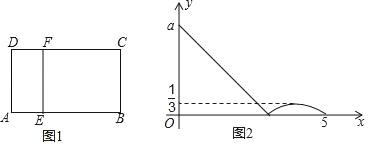
A. ЂйЂкЖМЖд B. ЂйЂкЖМДэ C. ЂйЖдЂкДэ D. ЂйДэЂкЖд
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
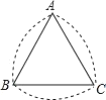
ЁОЬтФПЁПШчЙћЙигк![]() ЕФвЛдЊЖўДЮЗНГЬ
ЕФвЛдЊЖўДЮЗНГЬ![]() гаСНИіЪЕЪ§ИљЃЌЧвЦфжавЛИљЮЊСэвЛИљЕФ2БЖЃЌдђГЦетбљЕФЗНГЬЮЊЁАБЖИљЗНГЬЁБЃЌвдЯТЙигкБЖИљЗНГЬЕФЫЕЗЈЃЌВЛе§ШЗЕФЪЧЃЈ ЃЉ
гаСНИіЪЕЪ§ИљЃЌЧвЦфжавЛИљЮЊСэвЛИљЕФ2БЖЃЌдђГЦетбљЕФЗНГЬЮЊЁАБЖИљЗНГЬЁБЃЌвдЯТЙигкБЖИљЗНГЬЕФЫЕЗЈЃЌВЛе§ШЗЕФЪЧЃЈ ЃЉ
A.ЗНГЬ![]() ЪЧБЖИљЗНГЬЃЛ
ЪЧБЖИљЗНГЬЃЛ
B.Шє![]() ЪЧБЖИљЗНГЬЃЌдђ
ЪЧБЖИљЗНГЬЃЌдђ![]() ЃЛ
ЃЛ
C.ШєЗНГЬ![]() ЪЧБЖИљЗНГЬЃЌЧвЯрвьСНЕу
ЪЧБЖИљЗНГЬЃЌЧвЯрвьСНЕу![]() ЖМдкХзЮяЯп
ЖМдкХзЮяЯп![]() ЩЯЃЌдђЗНГЬ
ЩЯЃЌдђЗНГЬ![]() ЕФвЛИіИљЮЊ
ЕФвЛИіИљЮЊ![]() ЃЛ
ЃЛ
D.ШєЕу![]() дкЗДБШР§КЏЪ§
дкЗДБШР§КЏЪ§![]() ЕФЭМЯѓЩЯЃЌдђЙигк
ЕФЭМЯѓЩЯЃЌдђЙигк![]() ЕФЗНГЬ
ЕФЗНГЬ![]() ЪЧБЖИљЗНГЬЃЎ
ЪЧБЖИљЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com