
【题目】阅读下面的材料:
如果函数![]() 满足:对于自变量
满足:对于自变量![]() 的取值范围内的任意
的取值范围内的任意![]() ,
,![]() ,
,
(1)若![]() ,都有
,都有![]() ,则称
,则称![]() 是增函数;
是增函数;
(2)若![]() ,都有
,都有![]() ,则称
,则称![]() 是减函数.
是减函数.
例题:证明函数![]() 是减函数.
是减函数.
证明:设![]() ,
,
![]() .
.
∵![]() ,∴
,∴![]() ,
,![]() .∴
.∴![]() .即
.即![]() .
.
∴![]() .∴函数
.∴函数![]() (
(![]() )是减函数.
)是减函数.
根据以上材料,解答下面的问题:
己知函数![]() (
(![]() ),
),
(1)计算:![]() _______,
_______,![]() _______;
_______;
(2)猜想:函数![]() (
(![]() )是_______函数(填“增”或“减”);
)是_______函数(填“增”或“减”);
(3)请仿照例题证明你的猜想.
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
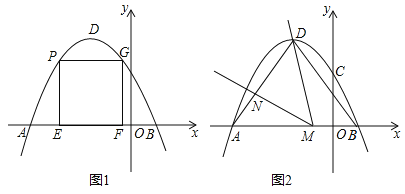
【题目】如图1,在平面直角坐标系中,抛物线y=-![]() x2+bx+c经过点A(-5,0)和点B(1,0).
x2+bx+c经过点A(-5,0)和点B(1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)点P是抛物线上A,D之间的一点,过点P作PE⊥x轴于点E,PG⊥y轴,交抛物线于点G.过点G作GF⊥x轴于点F.当矩形PEFG的周长最大时,求点P的横坐标;
(3)如图2,连接AD,BD,点M在线段AB上(不与A,B重合),作∠DMN=∠DBA,MN交线段AD于点N,是否存在这样的点M,使得△DMN为等腰三角形?若存在,求出AN的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,以
,以![]() 为坐标原点建立直角坚标系,使点
为坐标原点建立直角坚标系,使点![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() ,
,![]() ,点
,点![]() 为
为![]() 边的中点,抛物线的顶点是原点
边的中点,抛物线的顶点是原点![]() ,且经过
,且经过![]() 点
点
(1)填空:直线![]() 的解析式为 ;抛物线的解析式为 .
的解析式为 ;抛物线的解析式为 .
(2)现将该抛物线沿着线段![]() 移动,使其顶点
移动,使其顶点![]() 始终在线段
始终在线段![]() 上(包括点
上(包括点![]() ,
,![]() ),抛物线与
),抛物线与![]() 轴的交点为
轴的交点为![]() ,与
,与![]() 边的交点为
边的交点为![]() ;
;
①设![]() 的面积为
的面积为![]() ,求
,求![]() 的取值范围;
的取值范围;
②是否存在这样的点![]() ,使四边形
,使四边形![]() 为平行四边形?如存在,求出此时抛物线的解析式;如不存在,说明理由.
为平行四边形?如存在,求出此时抛物线的解析式;如不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年,随着电子产品的广泛应用,学生的近视发生率出现低龄化趋势,引起了相关部门的重视.某区为了了解在校学生的近视低龄化情况,对本区7-18岁在校近视学生进行了简单的随机抽样调查,并绘制了以下两幅不完整的统计图.

请根据图中信息,回答下列问题:
(1)这次抽样调查中共调查了近视学生 人;
(2)请补全条形统计图;
(3)扇形统计图中10-12岁部分的圆心角的度数是 ;
(4)据统计,该区7-18岁在校学生近视人数约为10万,请估计其中7-12岁的近视学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,C为⊙O上一点,BG与⊙O相切于点B,交AC的延长线于点D(点D在线段BG上),AC = 8,tan∠BDC =![]()
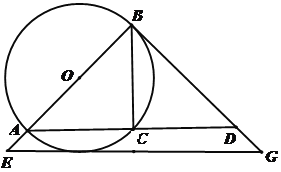
(1)求⊙O的直径;
(2)当DG=![]() 时,过G作
时,过G作![]() ,交BA的延长线于点E,说明EG与⊙O相切.
,交BA的延长线于点E,说明EG与⊙O相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,AB是直径,AP是过点A的切线,点C在
中,AB是直径,AP是过点A的切线,点C在![]() 上,点D在AP上,且
上,点D在AP上,且![]() ,延长DC交AB于点E.
,延长DC交AB于点E.
(1)求证:![]() .
.
(2)若![]() 的半径为5,
的半径为5,![]() ,求
,求![]() 的长.(结果保留
的长.(结果保留![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
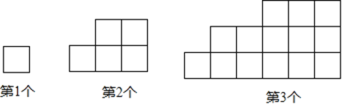
【题目】下列图形都是由大小相同的小正方形按一定规律组成的,其中第1个图形的周长为4,第2个图形的周长为10,第3个图形的周长为18,…,按此规律排列,回答下列问题:
(1)第5个图形的周长为 ;
(2)第![]() 个图形的周长为 ;
个图形的周长为 ;
(3)若第![]() 个图形的周长为180,则
个图形的周长为180,则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假旅游旺季即将到来,外出旅游的人数不断攀升,去海边游玩是大多数人不错的选择,去海边游玩的人都会选择自己购买海产品进行加工,某商家7月1日进购了一批扇贝与爬爬虾共计200千克,已知扇贝进价10元/千克,售价30元/千克,爬爬虾进价20元/千克,售价30元/千克.
(1)若这批海产品全部售完获利不低于3000元,则扇贝至少进购多少千克?
(2)第一批扇贝和爬爬虾很快售完,于是商家决定购进第二批扇贝与爬爬虾,两种海产品的进价不变,扇贝售价比第一批上涨![]() ,爬爬虾售价比第一批上涨
,爬爬虾售价比第一批上涨![]() ,销量与(1)中获得最低利润时的销量相比,扇贝的销量下降了
,销量与(1)中获得最低利润时的销量相比,扇贝的销量下降了![]() ,爬爬虾的销量不变,结果第二批已经卖掉的扇贝与爬爬虾的销售总额比(1)中第一批扇贝与爬爬虾售完后对应的最低销售总额增加了
,爬爬虾的销量不变,结果第二批已经卖掉的扇贝与爬爬虾的销售总额比(1)中第一批扇贝与爬爬虾售完后对应的最低销售总额增加了![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com