
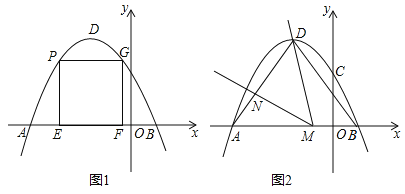
【题目】如图1,在平面直角坐标系中,抛物线y=-![]() x2+bx+c经过点A(-5,0)和点B(1,0).
x2+bx+c经过点A(-5,0)和点B(1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)点P是抛物线上A,D之间的一点,过点P作PE⊥x轴于点E,PG⊥y轴,交抛物线于点G.过点G作GF⊥x轴于点F.当矩形PEFG的周长最大时,求点P的横坐标;
(3)如图2,连接AD,BD,点M在线段AB上(不与A,B重合),作∠DMN=∠DBA,MN交线段AD于点N,是否存在这样的点M,使得△DMN为等腰三角形?若存在,求出AN的长;若不存在,请说明理由.
【答案】(1)y=-![]() x2-
x2-![]() x+
x+![]() ;D(-2,4);(2)点P的横坐标为-
;D(-2,4);(2)点P的横坐标为-![]() ;(3)存在,AN的长为1或
;(3)存在,AN的长为1或![]() .
.
【解析】
(1) 根据抛物线y=-![]() x2+bx+c经过点A(-5,0)和点B(1,0),用待定系数法即可得到答案;
x2+bx+c经过点A(-5,0)和点B(1,0),用待定系数法即可得到答案;
(2)假设P的坐标为(m,-![]() m2-
m2-![]() m+
m+![]() ),则可得到PE=-
),则可得到PE=-![]() m2-
m2-![]() m+
m+![]() ,PG=2(-2-m)=-4-2m,再结合矩形周长,即可算出答案;
,PG=2(-2-m)=-4-2m,再结合矩形周长,即可算出答案;
(3) 分三种情况MN=DM、NM=DN、DN=DM,分别讨论即可得到答案.
解:(1)抛物线的解析式为:y=-![]() (x+5)(x-1) =-
(x+5)(x-1) =-![]() x2-
x2-![]() x+
x+![]() .
.
配方得:y=-![]() (x+2)2+4 ,
(x+2)2+4 ,
∴顶点D的坐标为(-2,4).
(2)设点P的坐标为(m,-![]() m2-
m2-![]() m+
m+![]() ),
),
则PE=-![]() m2-
m2-![]() m+
m+![]() ,PG=2(-2-m)=-4-2m.
,PG=2(-2-m)=-4-2m.
∴矩形PEFG的周长=2(PE+PG)=2(-![]() m2-
m2-![]() m+
m+![]() -4-2m)
-4-2m)
=-![]() (m+
(m+![]() )2+
)2+![]() ,
,
∵-![]() <0,
<0,
∴当m=-![]() 时,矩形PEFG的周长最大,此时,点P的横坐标为-
时,矩形PEFG的周长最大,此时,点P的横坐标为-![]() .
.
(3)存在.∵AD=BD,
∴∠DAB=∠DBA.
∵∠AMN+∠DMN=∠MDB+∠DBA,
又∵∠DMN=∠DBA,
∴∠AMN=∠MDB,
∴△AMN∽△BDM,
∴![]() =
=![]() =
=![]() ,
,
易求得:AB=6,AD=DB=5.
△DMN为等腰三角形有三种可能:
①当MN=DM时,则△AMN≌△BDM,
∴AM=BD=5,
∴AN=MB=1;
②当DN=MN时,则∠ADM=∠DMN=∠DBA,
又∵∠DAM=∠BAD,
∴△DAM∽△BAD,
∴![]() =
=![]() ,
,
∴AD2=AM·BA.
∴AM=![]() ,BM=6-
,BM=6-![]() =
=![]() ,
,
∵![]() =
=![]() ,
,
∴AN=![]() =
=![]() ×
×![]() ×
×![]() =
=![]() .
.
③DN=DM不成立.
∵∠DNM>∠DAB, 而∠DAB=∠DMN,
∴∠DNM>∠DMN,
∴DN≠DM.
综上所述,存在点M满足要求,此时AN的长为1或![]() .
.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
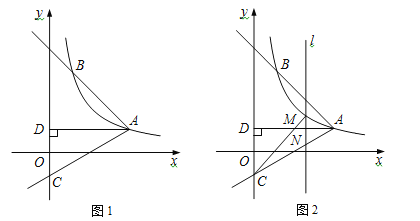
【题目】如图1,反比例函数![]() (x>0)的图象经过点A(
(x>0)的图象经过点A(![]() ,1),射线AB与反比例函数图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
,1),射线AB与反比例函数图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
(1)求k的值;
(2)求tan∠DAC的值及直线AC的解析式;
(3)如图2,M是线段AC上方反比例函数图象上一动点,过M作直线l⊥x轴,与AC相交于点N,连接CM,求△CMN面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校“心灵信箱”的设立,为师、生之间的沟通开设了一个书面交流的渠道.为了解九年级学生对“心灵信箱”开通两年来的使用情况,某课题组对该校九年级全体学生进行了一次问卷调查,并根据调查结果绘制了如下尚不完整的统计图.
两年来,你通过“心灵信箱”给老师总共投递过几封信? |
A.没投过 B.一封 C.两封 D.三封或以上 |
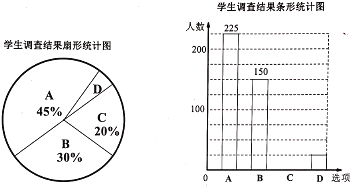
根据以上图表,解答下列问题:
(1)该校九年级学生共有____人;
(2)学生调查结果扇形统计图中,扇形![]() 的圆心角度数是______;
的圆心角度数是______;
(3)请你补全条形统计图;
(4)根据调查结果可以推断:两年来,该校九年级学生通过“心灵信箱”投递出信件总数至少有_____封.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知m,n是方程x2-6x+5=0的两个实数根,且m<n,抛物线
y=-x2+bx+c的图象经过点A(m,0)、B(0,n).
(1)求这个抛物线的解析式;
(2)设(1)中抛物线与x轴的另一交点为C,抛物线的顶点为D,试求出点C、D的坐标和△BCD的面积;
(3)P是线段OC上的一点,过点P作PH⊥x轴,与抛物线交于H点,若直线BC把△PCH分成面积之比为2:3的两部分,请求出P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
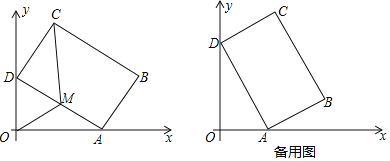
【题目】如图,在平面直角坐标系xOy中,矩形ABCD的边AB=4,BC=6.若不改变矩形ABCD的形状和大小,当矩形顶点A在x轴的正半轴上左右移动时,矩形的另一个顶点D始终在y轴的正半轴上随之上下移动.
(1)当∠OAD=30°时,求点C的坐标;
(2)设AD的中点为M,连接OM、MC,当四边形OMCD的面积为![]() 时,求OA的长;
时,求OA的长;
(3)当点A移动到某一位置时,点C到点O的距离有最大值,请直接写出最大值,并求此时cos∠OAD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
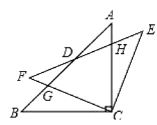
【题目】如图,△ABC中,BC=AC,∠ACB=90°,将△ABC绕着点C顺时针旋转α(0≤α≤90°),得到△EFC,EF与AB、AC相交于点D、H,FC与AB相交于点G、AC相交于点D、H,FC与AB相较于点G.
(1)求证:△GBC≌△HEC;
(2)在旋转过程中,当α是多少度时四边形BCED可以是某种特殊的平行四边形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将一块等腰直角三角板![]() 放在第二象限,斜靠在两坐标轴上
放在第二象限,斜靠在两坐标轴上![]() ,点
,点![]() 坐标为
坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,一次函数
,一次函数![]() 的图象经过点B、C,反比例函数
的图象经过点B、C,反比例函数![]() 的图象也经过点
的图象也经过点![]() .
.
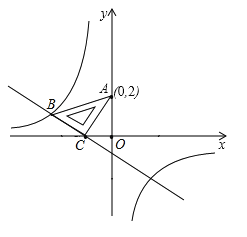
(1)求反比例函数和一次函数的关系式;
(2)观察图象直接写出图象在第二象限时,![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
如果函数![]() 满足:对于自变量
满足:对于自变量![]() 的取值范围内的任意
的取值范围内的任意![]() ,
,![]() ,
,
(1)若![]() ,都有
,都有![]() ,则称
,则称![]() 是增函数;
是增函数;
(2)若![]() ,都有
,都有![]() ,则称
,则称![]() 是减函数.
是减函数.
例题:证明函数![]() 是减函数.
是减函数.
证明:设![]() ,
,
![]() .
.
∵![]() ,∴
,∴![]() ,
,![]() .∴
.∴![]() .即
.即![]() .
.
∴![]() .∴函数
.∴函数![]() (
(![]() )是减函数.
)是减函数.
根据以上材料,解答下面的问题:
己知函数![]() (
(![]() ),
),
(1)计算:![]() _______,
_______,![]() _______;
_______;
(2)猜想:函数![]() (
(![]() )是_______函数(填“增”或“减”);
)是_______函数(填“增”或“减”);
(3)请仿照例题证明你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com