
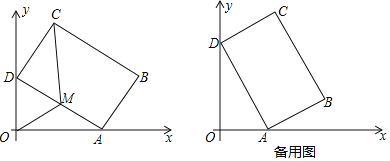
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌОиаЮABCDЕФБпABЃН4ЃЌBCЃН6ЃЎШєВЛИФБфОиаЮABCDЕФаЮзДКЭДѓаЁЃЌЕБОиаЮЖЅЕуAдкxжсЕФе§АыжсЩЯзѓгввЦЖЏЪБЃЌОиаЮЕФСэвЛИіЖЅЕуDЪМжедкyжсЕФе§АыжсЩЯЫцжЎЩЯЯТвЦЖЏЃЎ
(1)ЕБЁЯOADЃН30ЁуЪБЃЌЧѓЕуCЕФзјБъЃЛ
(2)ЩшADЕФжаЕуЮЊMЃЌСЌНгOMЁЂMCЃЌЕБЫФБпаЮOMCDЕФУцЛ§ЮЊ![]() ЪБЃЌЧѓOAЕФГЄЃЛ
ЪБЃЌЧѓOAЕФГЄЃЛ
(3)ЕБЕуAвЦЖЏЕНФГвЛЮЛжУЪБЃЌЕуCЕНЕуOЕФОрРыгазюДѓжЕЃЌЧыжБНгаДГізюДѓжЕЃЌВЂЧѓДЫЪБcosЁЯOADЕФжЕЃЎ
ЁОД№АИЁП(1)ЕуCЕФзјБъЮЊ(2ЃЌ3+2![]() )ЃЛ(2)OAЃН3
)ЃЛ(2)OAЃН3![]() ЃЛ(3)OCЕФзюДѓжЕЮЊ8ЃЌcosЁЯOADЃН
ЃЛ(3)OCЕФзюДѓжЕЮЊ8ЃЌcosЁЯOADЃН![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
(1)зїCEЁЭyжсЃЌЯШжЄЁЯCDEЃНЁЯOADЃН30ЁуЕУCEЃН![]() CDЃН2ЃЌDEЃН
CDЃН2ЃЌDEЃН![]() ЃЌдйгЩЁЯOADЃН30ЁужЊODЃН
ЃЌдйгЩЁЯOADЃН30ЁужЊODЃН![]() ADЃН3ЃЌДгЖјЕУГіЕуCзјБъЃЛ
ADЃН3ЃЌДгЖјЕУГіЕуCзјБъЃЛ
(2)ЯШЧѓГіSЁїDCMЃН6ЃЌНсКЯSЫФБпаЮOMCDЃН![]() жЊSЁїODMЃН
жЊSЁїODMЃН![]() ЃЌSЁїOADЃН9ЃЌЩшOAЃНxЁЂODЃНyЃЌОнДЫжЊx2+y2ЃН36ЃЌ
ЃЌSЁїOADЃН9ЃЌЩшOAЃНxЁЂODЃНyЃЌОнДЫжЊx2+y2ЃН36ЃЌ![]() xyЃН9ЃЌЕУГіx2+y2ЃН2xyЃЌМДxЃНyЃЌДњШыx2+y2ЃН36ЧѓЕУxЕФжЕЃЌДгЖјЕУГіД№АИЃЛ
xyЃН9ЃЌЕУГіx2+y2ЃН2xyЃЌМДxЃНyЃЌДњШыx2+y2ЃН36ЧѓЕУxЕФжЕЃЌДгЖјЕУГіД№АИЃЛ
(3)гЩMЮЊADЕФжаЕуЃЌжЊOMЃН3ЃЌCMЃН5ЃЌгЩOCЁмOM+CMЃН8жЊЕБOЁЂMЁЂCШ§ЕудкЭЌвЛжБЯпЪБЃЌOCгазюДѓжЕ8ЃЌСЌНгOCЃЌдђДЫЪБOCгыADЕФНЛЕуЮЊMЃЌONЁЭADЃЌжЄЁїCMDЁзЁїOMNЕУ![]() ЃЌОнДЫЧѓЕУMNЃН
ЃЌОнДЫЧѓЕУMNЃН![]() ЃЌONЃН
ЃЌONЃН![]() ЃЌANЃНAMЉMNЃН
ЃЌANЃНAMЉMNЃН![]() ЃЌдйгЩOAЃН
ЃЌдйгЩOAЃН![]() МАcosЁЯOADЃН
МАcosЁЯOADЃН![]() ПЩЕУД№АИЃЎ
ПЩЕУД№АИЃЎ
(1)ШчЭМ1ЃЌЙ§ЕуCзїCEЁЭyжсгкЕуEЃЌ
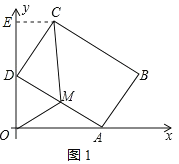
ЁпОиаЮABCDжаЃЌCDЁЭADЃЌ
ЁрЁЯCDE+ЁЯADOЃН90ЁуЃЌ
гжЁпЁЯOAD+ЁЯADOЃН90ЁуЃЌ
ЁрЁЯCDEЃНЁЯOADЃН30ЁуЃЌ
ЁрдкRtЁїCEDжаЃЌCEЃН![]() CDЃН2ЃЌDEЃН
CDЃН2ЃЌDEЃН![]() ЃН2
ЃН2![]() ЃЌ
ЃЌ
дкRtЁїOADжаЃЌЁЯOADЃН30ЁуЃЌ
ЁрODЃН![]() ADЃН3ЃЌ
ADЃН3ЃЌ
ЁрЕуCЕФзјБъЮЊ(2ЃЌ3+2![]() )ЃЛ
)ЃЛ
(2)ЁпMЮЊADЕФжаЕуЃЌ
ЁрDMЃН3ЃЌSЁїDCMЃН6ЃЌ
гжSЫФБпаЮOMCDЃН![]() ЃЌ
ЃЌ
ЁрSЁїODMЃН![]() ЃЌ
ЃЌ
ЁрSЁїOADЃН9ЃЌ
ЩшOAЃНxЁЂODЃНyЃЌдђx2+y2ЃН36ЃЌ![]() xyЃН9ЃЌ
xyЃН9ЃЌ
Ёрx2+y2ЃН2xyЃЌМДxЃНyЃЌ
НЋxЃНyДњШыx2+y2ЃН36ЕУx2ЃН18ЃЌ
НтЕУxЃН3![]() (ИКжЕЩсШЅ)ЃЌ
(ИКжЕЩсШЅ)ЃЌ
ЁрOAЃН3![]() ЃЛ
ЃЛ
(3)OCЕФзюДѓжЕЮЊ8ЃЌ
ШчЭМ2ЃЌMЮЊADЕФжаЕуЃЌ
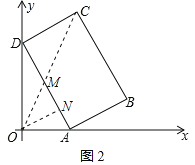
ЁрOMЃН3ЃЌCMЃН![]() ЃН5ЃЌ
ЃН5ЃЌ
ЁрOCЁмOM+CMЃН8ЃЌ
ЕБOЁЂMЁЂCШ§ЕудкЭЌвЛжБЯпЪБЃЌOCгазюДѓжЕ8ЃЌ
СЌНгOCЃЌдђДЫЪБOCгыADЕФНЛЕуЮЊMЃЌЙ§ЕуOзїONЁЭADЃЌДЙзуЮЊNЃЌ
ЁпЁЯCDMЃНЁЯONMЃН90ЁуЃЌЁЯCMDЃНЁЯOMNЃЌ
ЁрЁїCMDЁзЁїOMNЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
НтЕУMNЃН![]() ЃЌONЃН
ЃЌONЃН![]() ЃЌ
ЃЌ
ЁрANЃНAMЉMNЃН![]() ЃЌ
ЃЌ
дкRtЁїOANжаЃЌOAЃН![]() ЃЌ
ЃЌ
ЁрcosЁЯOADЃН![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
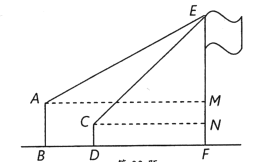
ЁОЬтФПЁПШчЭМЃЌФГЪ§бЇаЫШЄаЁзщдкЛюЖЏПЮЩЯВтСПбЇаЃЦьИЫЕФИпЖШЃЎвбжЊаЁССеОзХВтСПЃЌблОІгыЕиУцЕФОрРыЃЈABЃЉЪЧ1.6УзЃЌПДЦьИЫЖЅВПEЕФбіНЧЮЊ30ЁуЃЛаЁУєЖззХВтСПЃЌблОІгыЕиУцЕФОрРыЃЈCDЃЉЪЧ0.6УзЃЌПДЦьИЫЖЅВПEЕФбіНЧЮЊ45Ёу.СНШЫЯрОр5УзЧвЮЛгкЦьИЫЭЌВрЃЈЕуBЁЂDЁЂFдкЭЌвЛжБЯпЩЯЃЉЃЎЧѓЦьИЫEFЕФИпЖШЃЎЃЈНсЙћБЃСєИљКХЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,КЏЪ§![]() КЭ
КЭ![]() (
(![]() ЪЧГЃЪ§,Чв
ЪЧГЃЪ§,Чв![]() )дкЭЌвЛЦНУцжБНЧзјБъЯЕЕФЭМЯѓПЩФмЪЧЃЈ ЃЉ
)дкЭЌвЛЦНУцжБНЧзјБъЯЕЕФЭМЯѓПЩФмЪЧЃЈ ЃЉ
A.  B.
B. 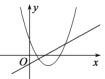 C.
C. 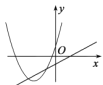 D.
D. 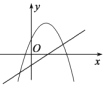
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDжаЃЌABЃН3![]() ЃЌBCЃН12ЃЌEЮЊADжаЕуЃЌFЮЊABЩЯвЛЕуЃЌНЋЁїAEFбиEFелЕўКѓЃЌЕуAЧЁКУТфЕНCFЩЯЕФЕуGДІЃЌдђелКлEFЕФГЄЪЧ_____ЃЎ
ЃЌBCЃН12ЃЌEЮЊADжаЕуЃЌFЮЊABЩЯвЛЕуЃЌНЋЁїAEFбиEFелЕўКѓЃЌЕуAЧЁКУТфЕНCFЩЯЕФЕуGДІЃЌдђелКлEFЕФГЄЪЧ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
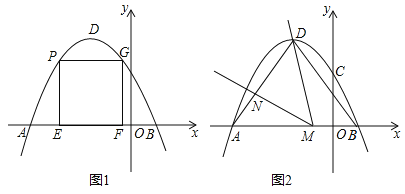
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпyЃНЃ![]() x2ЃЋbxЃЋcОЙ§ЕуA(Ѓ5ЃЌ0)КЭЕуB(1ЃЌ0)ЃЎ
x2ЃЋbxЃЋcОЙ§ЕуA(Ѓ5ЃЌ0)КЭЕуB(1ЃЌ0)ЃЎ
(1)ЧѓХзЮяЯпЕФНтЮіЪНМАЖЅЕуDЕФзјБъЃЛ
(2)ЕуPЪЧХзЮяЯпЩЯAЃЌDжЎМфЕФвЛЕуЃЌЙ§ЕуPзїPEЁЭxжсгкЕуEЃЌPGЁЭyжсЃЌНЛХзЮяЯпгкЕуGЃЎЙ§ЕуGзїGFЁЭxжсгкЕуFЃЎЕБОиаЮPEFGЕФжмГЄзюДѓЪБЃЌЧѓЕуPЕФКсзјБъЃЛ
(3)ШчЭМ2ЃЌСЌНгADЃЌBDЃЌЕуMдкЯпЖЮABЩЯ(ВЛгыAЃЌBжиКЯ)ЃЌзїЁЯDMNЃНЁЯDBAЃЌMNНЛЯпЖЮADгкЕуNЃЌЪЧЗёДцдкетбљЕФЕуMЃЌЪЙЕУЁїDMNЮЊЕШбќШ§НЧаЮЃПШєДцдкЃЌЧѓГіANЕФГЄЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ12ЗжЃЉШчЭМ1ЃЌЕуOЪЧе§ЗНаЮABCDСНЖдНЧЯпЕФНЛЕуЃЌЗжБ№бгГЄODЕНЕуGЃЌOCЕНЕуEЃЌЪЙOG=2ODЃЌOE=2OCЃЌШЛКѓвдOGЁЂOEЮЊСкБпзїе§ЗНаЮOEFGЃЌСЌНгAGЃЌDEЃЎ

ЃЈ1ЃЉЧѓжЄЃКDEЁЭAGЃЛ
ЃЈ2ЃЉе§ЗНаЮABCDЙЬЖЈЃЌНЋе§ЗНаЮOEFGШЦЕуOФцЪБеыа§зЊІСНЧЃЈ0ЁуЃМІСЃМ360ЁуЃЉЕУЕНе§ЗНаЮOEЁфFЁфGЁфЃЌШчЭМ2ЃЎ
Ђйдка§зЊЙ§ГЬжаЃЌЕБЁЯOAGЁфЪЧжБНЧЪБЃЌЧѓІСЕФЖШЪ§ЃЛ
ЂкШєе§ЗНаЮABCDЕФБпГЄЮЊ1ЃЌдка§зЊЙ§ГЬжаЃЌЧѓAFЁфГЄЕФзюДѓжЕКЭДЫЪБІСЕФЖШЪ§ЃЌжБНгаДГіНсЙћВЛБиЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЧѓЖўДЮКЏЪ§![]() ЕФЭМЯѓШчЭМЫљЪОЃЌЦфЖдГЦжсЮЊжБЯп
ЕФЭМЯѓШчЭМЫљЪОЃЌЦфЖдГЦжсЮЊжБЯп![]() ЃЌгы
ЃЌгы![]() жсЕФНЛЕуЮЊ
жсЕФНЛЕуЮЊ![]() ЁЂ
ЁЂ![]() ЃЌЦфжа
ЃЌЦфжа![]() ЃЌгаЯТСаНсТлЃКЂй
ЃЌгаЯТСаНсТлЃКЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЃЛЂм
ЃЛЂм![]() ЃЛЂн
ЃЛЂн![]() ЃЛЦфжаЃЌе§ШЗЕФНсТлгаЃЈ ЃЉ
ЃЛЦфжаЃЌе§ШЗЕФНсТлгаЃЈ ЃЉ
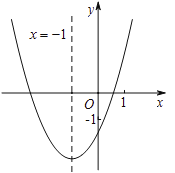
A.5B.4C.3D.2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
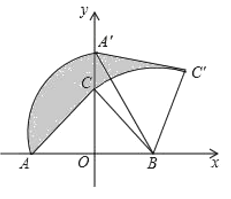
ЁОЬтФПЁПШчЭМЃЌRtЁїABCжаЃЌЁЯACBЃН90ЁуЃЌACЃНBCЃЌдквдABЕФжаЕуOЮЊзјБъдЕуЃЌABЫљдкжБЯпЮЊxжсНЈСЂЕФЦНУцжБНЧзјБъЯЕжаЃЌНЋЁїABCШЦЕуBЫГЪБеыа§зЊЃЌЪЙЕуAа§зЊжСyжсЕФе§АыжсЩЯЕФЕуA'ДІЃЌШєAOЃНOBЃН2ЃЌдђЭМжавѕгАВПЗжУцЛ§ЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊABЮЊЁбOЕФжБОЖЃЌCЮЊЁбOЩЯвЛЕуЃЌBGгыЁбOЯрЧагкЕуBЃЌНЛACЕФбгГЄЯпгкЕуDЃЈЕуDдкЯпЖЮBGЩЯЃЉЃЌAC = 8ЃЌtanЁЯBDC =![]()
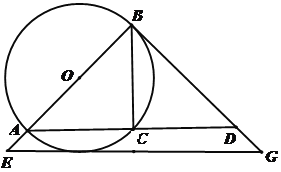
ЃЈ1ЃЉЧѓЁбOЕФжБОЖЃЛ
ЃЈ2ЃЉЕБDG=![]() ЪБЃЌЙ§Gзї
ЪБЃЌЙ§Gзї![]() ЃЌНЛBAЕФбгГЄЯпгкЕуEЃЌЫЕУїEGгыЁбOЯрЧаЃЎ
ЃЌНЛBAЕФбгГЄЯпгкЕуEЃЌЫЕУїEGгыЁбOЯрЧаЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com