
【题目】如图,△ABC中,BC=AC,∠ACB=90°,将△ABC绕着点C顺时针旋转α(0≤α≤90°),得到△EFC,EF与AB、AC相交于点D、H,FC与AB相交于点G、AC相交于点D、H,FC与AB相较于点G.
(1)求证:△GBC≌△HEC;
(2)在旋转过程中,当α是多少度时四边形BCED可以是某种特殊的平行四边形?并说明理由.
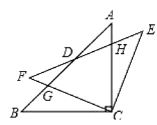
【答案】(1)详见解析;(2)当α=45°时,四边形BCED为菱形,理由详见解析.
【解析】
(1)先判断△ABC为等腰直角三角形得到∠A=∠B=45°,再由旋转的性质得到∠BCF=∠ACE=α,∠E=∠A=45°,CA=CE=CB,最后可根据“ASA”可判断△GBC≌△HEC;
(2)当α=45°时,根据旋转的性质得∠BCF=∠ACE=45°,则可计算出∠BCE=∠BCA+∠ACE=135°,再证BD∥CE,BC∥DE,于是可判断四边形BCED为平行四边形,结合CB=CE,则可判断四边形BCED为菱形.
解:(1)证明:∵BC=AC,∠ACB=90°,
∴△ABC为等腰直角三角形,
∴∠A=∠B=45°,
∵△ABC绕着点C顺时针旋转α°(0≤α≤90°),得到△EFC,
∴∠BCF=∠ACE=α,∠E=∠A=45°,CA=CE=CB,
在△GBC和△HEC中
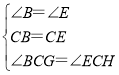
∴△GBC≌△HEC(ASA);
(2)解:当α=45°时,四边形BCED为菱形.理由如下:
如图,
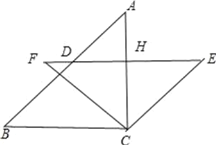
∵∠BCF=∠ACE=45°,
∴∠BCE=∠BCA+∠ACE=90°+45°=135°,
而∠E=∠B=45°,
∴∠B+∠BCE=180°,∠E+∠BCE=180°,
∴BD∥CE,BC∥DE(同旁内角互补,两直线平行),
∴四边形BCED为平行四边形,
∵CB=CE,
∴四边形BCED为菱形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]()
![]() 当抛物线的顶点在
当抛物线的顶点在![]() 轴上时,求该抛物线的解析式;
轴上时,求该抛物线的解析式;
![]() 不论
不论![]() 取何值时,抛物线的顶点始终在一条直线上,求该直线的解析式;
取何值时,抛物线的顶点始终在一条直线上,求该直线的解析式;
![]() 若有两点
若有两点![]() ,
,![]() ,且该抛物线与线段
,且该抛物线与线段![]() 始终有交点,请直接写出
始终有交点,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
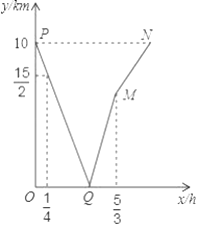
【题目】甲、乙两人分别从A,B两地同时出发,匀速相向而行.甲的速度大于乙的速度,甲到达B地后,乙继续前行.设出发x h后,两人相距y km,图中折线表示从两人出发至乙到达A地的过程中y与x之间的函数关系.
根据图中信息,求:
(1)点Q的坐标,并说明它的实际意义;
(2)甲、乙两人的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
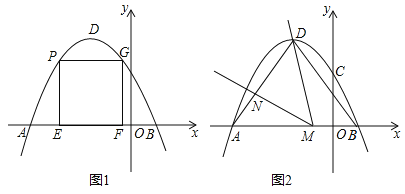
【题目】如图1,在平面直角坐标系中,抛物线y=-![]() x2+bx+c经过点A(-5,0)和点B(1,0).
x2+bx+c经过点A(-5,0)和点B(1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)点P是抛物线上A,D之间的一点,过点P作PE⊥x轴于点E,PG⊥y轴,交抛物线于点G.过点G作GF⊥x轴于点F.当矩形PEFG的周长最大时,求点P的横坐标;
(3)如图2,连接AD,BD,点M在线段AB上(不与A,B重合),作∠DMN=∠DBA,MN交线段AD于点N,是否存在这样的点M,使得△DMN为等腰三角形?若存在,求出AN的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队共同承担一项筑路任务,甲队单独施工完成此项任务比乙队单独施工完成此项任务多用![]() 天,且甲队单独施工
天,且甲队单独施工![]() 天和乙队单独施工
天和乙队单独施工![]() 天的工作量相同.
天的工作量相同.
![]() 甲、乙两队单独完成此项任务各需多少天?
甲、乙两队单独完成此项任务各需多少天?
![]() 设先由甲队施工
设先由甲队施工![]() 天,再由乙队施工
天,再由乙队施工![]() 天,刚好完成筑路任务,求
天,刚好完成筑路任务,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
![]() 在
在![]() 的条件下,若每天需付给甲队的筑路费用为
的条件下,若每天需付给甲队的筑路费用为![]() 万元,需付给乙队的筑路费用为
万元,需付给乙队的筑路费用为![]() 万元,且甲、乙两队施工的总天数不超过
万元,且甲、乙两队施工的总天数不超过![]() 天,则如何安排甲、乙两队施工的天数,使施工费用最少,并求出最少费用.
天,则如何安排甲、乙两队施工的天数,使施工费用最少,并求出最少费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求二次函数![]() 的图象如图所示,其对称轴为直线
的图象如图所示,其对称轴为直线![]() ,与
,与![]() 轴的交点为
轴的交点为![]() 、
、![]() ,其中
,其中![]() ,有下列结论:①
,有下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ;其中,正确的结论有( )
;其中,正确的结论有( )
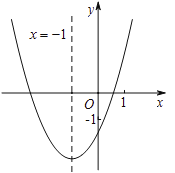
A.5B.4C.3D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等腰Rt△ABC中,∠A=90°,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.

(1)观察猜想:图1中,线段PM与PN的数量关系是 ,位置关系是 ;
(2)探究证明:把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=8,AB=20,请直接写出△PMN面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,以
,以![]() 为坐标原点建立直角坚标系,使点
为坐标原点建立直角坚标系,使点![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() ,
,![]() ,点
,点![]() 为
为![]() 边的中点,抛物线的顶点是原点
边的中点,抛物线的顶点是原点![]() ,且经过
,且经过![]() 点
点
(1)填空:直线![]() 的解析式为 ;抛物线的解析式为 .
的解析式为 ;抛物线的解析式为 .
(2)现将该抛物线沿着线段![]() 移动,使其顶点
移动,使其顶点![]() 始终在线段
始终在线段![]() 上(包括点
上(包括点![]() ,
,![]() ),抛物线与
),抛物线与![]() 轴的交点为
轴的交点为![]() ,与
,与![]() 边的交点为
边的交点为![]() ;
;
①设![]() 的面积为
的面积为![]() ,求
,求![]() 的取值范围;
的取值范围;
②是否存在这样的点![]() ,使四边形
,使四边形![]() 为平行四边形?如存在,求出此时抛物线的解析式;如不存在,说明理由.
为平行四边形?如存在,求出此时抛物线的解析式;如不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,AB是直径,AP是过点A的切线,点C在
中,AB是直径,AP是过点A的切线,点C在![]() 上,点D在AP上,且
上,点D在AP上,且![]() ,延长DC交AB于点E.
,延长DC交AB于点E.
(1)求证:![]() .
.
(2)若![]() 的半径为5,
的半径为5,![]() ,求
,求![]() 的长.(结果保留
的长.(结果保留![]() )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com