
����Ŀ����ͼ��![]() �У�
��![]() ����
����![]() Ϊ����ԭ�㽨��ֱ�Ǽ��ϵ��ʹ��
Ϊ����ԭ�㽨��ֱ�Ǽ��ϵ��ʹ��![]() ��
��![]() ���������ϣ�
���������ϣ�![]() ��
��![]() ����
����![]() Ϊ
Ϊ![]() �ߵ��е㣬�����ߵĶ�����ԭ��
�ߵ��е㣬�����ߵĶ�����ԭ��![]() ���Ҿ���
���Ҿ���![]() ��
��
(1)��գ�ֱ��![]() �Ľ���ʽΪ �������ߵĽ���ʽΪ ��
�Ľ���ʽΪ �������ߵĽ���ʽΪ ��
(2)�ֽ��������������߶�![]() �ƶ���ʹ�䶥��
�ƶ���ʹ�䶥��![]() ʼ�����߶�
ʼ�����߶�![]() ��(������
��(������![]() ��
��![]() )����������
)����������![]() ��Ľ���Ϊ
��Ľ���Ϊ![]() ����
����![]() �ߵĽ���Ϊ
�ߵĽ���Ϊ![]() ��
��
����![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���Ƿ���������ĵ�![]() ��ʹ�ı���
��ʹ�ı���![]() Ϊƽ���ı��Σ�����ڣ������ʱ�����ߵĽ���ʽ���粻���ڣ�˵�����ɣ�
Ϊƽ���ı��Σ�����ڣ������ʱ�����ߵĽ���ʽ���粻���ڣ�˵�����ɣ�

���𰸡���1��y=2x��y=x2 ����2����![]() ���ڴ��ڣ�
���ڴ��ڣ�![]()
��������
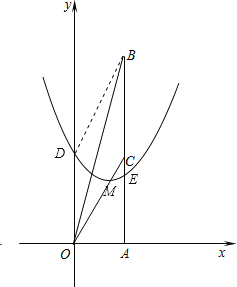
��1���������������C������Ȼ�����ֱ��OC�Ľ���ʽ�������ߵĽ���ʽ��
��2���ٸ��������ߵ��ƶ�������������ߵĽ���ʽ�������BOE�����S��m�Ĺ�ϵ���ٸ���m��ȡֵ��Χ�������S��ȡֵ��Χ��
�ڸ���ƽ���ı��ε����ʼ��ɵó�m��ֵ��
�⣺��1����OA=2��AB=8����CΪAB�ߵ��е㣬
���C������Ϊ��2��4���㣬
��ֱ�ߵĽ���ʽΪy=kx
��4=2k�����k=2
��ֱ�ߵĽ���ʽΪy=2x��
�������ߵĽ���ʽΪy=kx2
��4=4k�����k=1
�������ߵĽ���ʽΪy=x2��
��2�����ƶ��������ߵĽ���ʽΪy=��x-m��2+2m��
�� ��![]() ��
��
![]()
![]()
![]()
![]() ��
��
�֡�![]() ��
��
��![]() ��
��
�ڴ��ڵ�D��ʹ�ı���BDOCΪƽ���ı��Σ�
��OD=BC���ı���BDOCΪƽ���ı��Σ�
��OD=BC=![]() =4��
=4��
��ɵ�x=0ʱy=4��
��m2+2m=4��
�ࣨm+1��2=5��
���![]() ��
��![]() ����ȥ����
����ȥ����
����![]() ��
��
��![]()
![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��������������������Ϊʦ����֮��Ĺ�ͨ������һ�����潻��������.Ϊ�˽���꼶ѧ������������������ͨ��������ʹ�������ij������Ը�У���꼶ȫ��ѧ��������һ���ʾ����飬�����ݵ����������������в�������ͳ��ͼ.
����������ͨ������������������ʦ�ܹ�Ͷ�ݹ������ţ� |
A.ûͶ�� B.һ�� C.���� D.��������� |
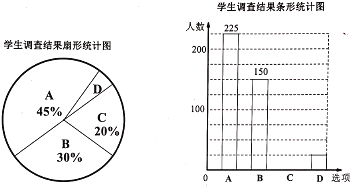
��������ͼ��������������⣺
(1)��У���꼶ѧ������____�ˣ�
(2)ѧ������������ͳ��ͼ�У�����![]() ��Բ�ĽǶ�����______��
��Բ�ĽǶ�����______��
(3)���㲹ȫ����ͳ��ͼ��
(4)���ݵ����������ƶϣ�����������У���꼶ѧ��ͨ��������������Ͷ�ݳ��ż�����������_____��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
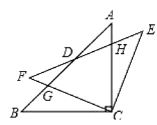
����Ŀ����ͼ����ABC�У�BC=AC����ACB=90��������ABC���ŵ�C˳ʱ����ת����0������90�������õ���EFC��EF��AB��AC�ཻ�ڵ�D��H��FC��AB�ཻ�ڵ�G��AC�ཻ�ڵ�D��H��FC��AB����ڵ�G��
��1����֤����GBC�ա�HEC��
��2������ת�����У������Ƕ��ٶ�ʱ�ı���BCED������ij�������ƽ���ı��Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���һ�����ֱ�����ǰ�![]() ���ڵڶ����ޣ�б��������������
���ڵڶ����ޣ�б��������������![]() ����
����![]() ����Ϊ
����Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() ��һ�κ���
��һ�κ���![]() ��ͼ����B��C������������
��ͼ����B��C������������![]() ��ͼ��Ҳ������
��ͼ��Ҳ������![]() ��
��
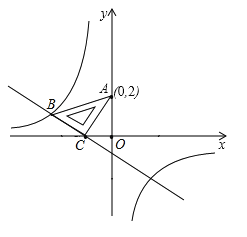
(1)����������һ�κ����Ĺ�ϵʽ��
(2)�۲�ͼ��ֱ��д��ͼ���ڵڶ�����ʱ��![]() �Ľ⼯��
�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
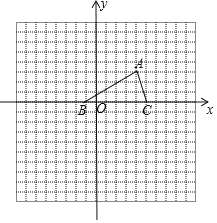
����Ŀ����ͼ����֪��ABC���������������ֱ�ΪA��3��3����B����1��0����C��4��0����
��1������ƽ�ƣ���ʹ��ABC�Ķ���A������ԭ��O�غϣ����C�Ķ�Ӧ��C1������Ϊ�� ���������û�ͼ��
��2����ͼ�л�������ABC�Ƶ�B��ʱ����ת90��õ��ġ�A��BC�䣻
��3���Ե�AΪλ�����ķŴ��ABC���õ���AB2C2��ʹS��ABC��S![]() ��1��4����ͼ�л�����AB2C2��
��1��4����ͼ�л�����AB2C2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
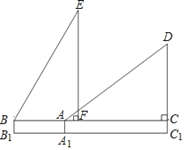
����Ŀ����ͼ��С����һ�ηŷ��ݻ��ijʱ�ε�ʾ��ͼ������A��ʱ�ķ�����(���������з����߽��Ƶؿ���ֱ��)��ˮƽ�߹���37��ǣ��߶�AA1��ʾС������1.5�ף������ӵ�A�ܶ�4�����B��ʱ����������ˮƽ�߹���60��ǣ���ʱ���ݵ����E�������ݵ�ˮƽ�ƶ�����CFΪ8�ף���һ�����з����ߵij��ȱ��ֲ��䣬�����ԭ���ĸ߶�C1D��
(�ο����ݣ�sin37���0.6��cos37���0.8��tan37���0.75��)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
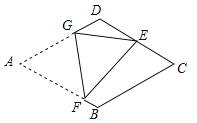
����Ŀ����ͼ��������ABCD�У�AB��2����D��120�㣬�����η��ۣ�ʹ��A���ڱ�CD���е�E�����ۺ۽���AD��AB�ڵ�G��F����AF�ij�Ϊ___
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�����IJ��ϣ�
�������![]() ���㣺�����Ա���
���㣺�����Ա���![]() ��ȡֵ��Χ�ڵ�����
��ȡֵ��Χ�ڵ�����![]() ��
��![]() ��
��
��1����![]() ������
������![]() �����
�����![]() ����������
����������
��2����![]() ������
������![]() �����
�����![]() �Ǽ�������
�Ǽ�������
���⣺֤������![]() �Ǽ�������
�Ǽ�������
֤������![]() ��
��
![]() ��
��
��![]() ����
����![]() ��
��![]() ����
����![]() ����
����![]() ��
��
��![]() ���ຯ��
���ຯ��![]() ��
��![]() ���Ǽ�������
���Ǽ�������
�������ϲ��ϣ������������⣺
��֪����![]() ��
��![]() ����
����
��1�����㣺![]() _______��
_______��![]() _______��
_______��
��2�����룺����![]() ��
��![]() ����_______�������������������
����_______�������������������
��3�����������֤����IJ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y��x2+bx+c��ͼ����A(��1��0)��B(0����3)��
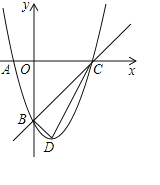
��1������������ߵĽ���ʽ��
��2����������x�����һ����ΪC�������ߵĶ���ΪD���ж���CBD����״��
��3��ֱ��BN��x�ᣬ������������һ��N����P��ֱ��BN�·����������ϵ�һ�����㣨��P�����B�͵�N�غϣ�������P��x��Ĵ��ߣ���ֱ��BC�ڵ�Q�����ı���BPNQ��������ʱ�������P�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com