
【题目】如果关于![]() 的一元二次方程
的一元二次方程![]() 有两个实数根,且其中一根为另一根的2倍,则称这样的方程为“倍根方程”,以下关于倍根方程的说法,不正确的是( )
有两个实数根,且其中一根为另一根的2倍,则称这样的方程为“倍根方程”,以下关于倍根方程的说法,不正确的是( )
A.方程![]() 是倍根方程;
是倍根方程;
B.若![]() 是倍根方程,则
是倍根方程,则![]() ;
;
C.若方程![]() 是倍根方程,且相异两点
是倍根方程,且相异两点![]() 都在抛物线
都在抛物线![]() 上,则方程
上,则方程![]() 的一个根为
的一个根为![]() ;
;
D.若点![]() 在反比例函数
在反比例函数![]() 的图象上,则关于
的图象上,则关于![]() 的方程
的方程![]() 是倍根方程.
是倍根方程.
【答案】C
【解析】
A、根据倍根方程定义即可得到方程x2+3x+2=0是倍根方程;
B、根据(x-2)(mx+n)=0是倍根方程,且x1=2,x2=![]() 得到
得到![]() =-1或
=-1或![]() =-4,从而得到m+n=0,或4m+n=0,进而得到4m2+5mn+n2=(4m+n)(m+n)=0正确;
=-4,从而得到m+n=0,或4m+n=0,进而得到4m2+5mn+n2=(4m+n)(m+n)=0正确;
C、由方程ax2+bx+c=0是倍根方程,得到x1=2x2,有已知条件得到得到抛物线的对称轴x=![]() ,可得x1和x2的值,可作判断.
,可得x1和x2的值,可作判断.
D、根据已知条件得到pq=2,解方程px2+3x+q=0得到方程的根;
x2+3x+2=0,
(x+1)(x+2)=0,
x1=-1,x2=-2,
∴方程x2+3x+2=0是倍根方程;
故A正确;
解方程(x-2)(mx+n)=0,
得:x1=2,x2=![]() ,
,
∵(x-2)(mx+n)=0是倍根方程,
∴![]() =-1或
=-1或![]() =-4,
=-4,
∴m+n=0或4m+n=0,
∵4m2+5mn+n2=(4m+n)(m+n)=0,
故B正确;
∵方程ax2+bx+c=0是倍根方程,
∴设x1=2x2,
∵相异两点M(1+t,s),N(4-t,s)都在抛物线y=ax2+bx+c上,
∴抛物线的对称轴x=![]() ,
,
∴x1+x2=5,
∴x2+2x2=5,
∴x1=![]() , x2=
, x2=![]()
故C不正确;
∵点(p,q)在反比例函数![]() 的图象上,
的图象上,
∴pq=2,
解方程px2+3x+q=0得:
x1=![]() ,x2=
,x2=![]() ,
,
∴x2=2x1,故D正确.
故选:C.


科目:初中数学 来源: 题型:
【题目】暑假旅游旺季即将到来,外出旅游的人数不断攀升,去海边游玩是大多数人不错的选择,去海边游玩的人都会选择自己购买海产品进行加工,某商家7月1日进购了一批扇贝与爬爬虾共计200千克,已知扇贝进价10元/千克,售价30元/千克,爬爬虾进价20元/千克,售价30元/千克.
(1)若这批海产品全部售完获利不低于3000元,则扇贝至少进购多少千克?
(2)第一批扇贝和爬爬虾很快售完,于是商家决定购进第二批扇贝与爬爬虾,两种海产品的进价不变,扇贝售价比第一批上涨![]() ,爬爬虾售价比第一批上涨
,爬爬虾售价比第一批上涨![]() ,销量与(1)中获得最低利润时的销量相比,扇贝的销量下降了
,销量与(1)中获得最低利润时的销量相比,扇贝的销量下降了![]() ,爬爬虾的销量不变,结果第二批已经卖掉的扇贝与爬爬虾的销售总额比(1)中第一批扇贝与爬爬虾售完后对应的最低销售总额增加了
,爬爬虾的销量不变,结果第二批已经卖掉的扇贝与爬爬虾的销售总额比(1)中第一批扇贝与爬爬虾售完后对应的最低销售总额增加了![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 是
是![]() 轴正半轴上的一动点,抛物线
轴正半轴上的一动点,抛物线![]() (
(![]() 是常数,且
是常数,且![]() 过点
过点![]() ,与
,与![]() 轴交于
轴交于![]() 两点,点
两点,点![]() 在点
在点![]() 左侧,连接
左侧,连接![]() ,以
,以![]() 为边做等边三角形
为边做等边三角形![]() ,点
,点![]() 与点
与点![]() 在直线
在直线![]() 两侧.
两侧.
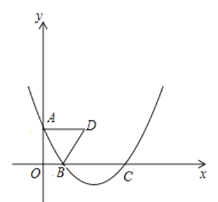
(1)求B、C的坐标;
(2)当![]() 轴时,求抛物线的函数表达式;
轴时,求抛物线的函数表达式;
(3)①求动点![]() 所成的图像的函数表达式;
所成的图像的函数表达式;
②连接![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M是矩形ABCD的边AD的中点,点P是BC边上一动点,PE⊥MC,PF⊥BM,垂足为E、F.
(1)当矩形ABCD的长与宽满足什么条件时,四边形PEMF为矩形?猜想并证明你的结论.
(2)在(1)中,当点P运动到什么位置时,矩形PEMF变为正方形,为什么?
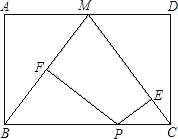
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABE和△ACF中,EB交AC于点M,交FC于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF.下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中,正确的是_________.(填序号)
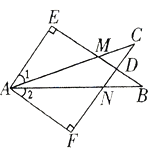
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着网购的日益盛行,物流行业已逐渐成为运输业的主力,已知某大型物流公司有A、B两种型号的货车,A型货车的满载量是B型货车满载量的2倍多4吨,在两车满载的情况下,用A型货车载1400吨货物与用B型货车载560吨货物的用车数量相同.
(1)1辆A型货车和1辆B型货车的满载量分别是多少?
(2)该物流公司现有120吨货物,可以选择上述两种货车运送,在满载的情况下,有几种方案可以一次性运完?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为配合“一带一路”国家倡议,某铁路货运集装箱物流园区正式启动了2期扩建工程一项地基基础加固处理工程由2、8两个工程公司承担建设,己知2工程公司单独建设完成此项工程需要180天![]() 工程公司单独施工天后,
工程公司单独施工天后,![]() 工程公司参与合作,两工程公司又共同施工
工程公司参与合作,两工程公司又共同施工![]() 天后完成了此项工程.
天后完成了此项工程.
(1)求![]() 工程公司单独建设完成此项工程需要多少天?
工程公司单独建设完成此项工程需要多少天?
(2)由于受工程建设工期的限制,物流园区管委会决定将此项工程划包成两部分,要求两工程公司同时开工,![]() 工程公司建设其中一部分用了
工程公司建设其中一部分用了![]() 天完成,
天完成,![]() 工程公司建设另一部分用了
工程公司建设另一部分用了![]() 天完成,其中
天完成,其中![]() ,
,![]() 均为正整数,且
均为正整数,且![]() ,
,![]() ,求
,求![]() 、
、![]() 两个工程公司各施工建设了多少天?
两个工程公司各施工建设了多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“综合与实践”是以问题为中心,以活动为平台,以解决某一实际的数学问题为目标,综合应用知识和方法解决问题,它是对数学知识的延伸和发展,是对理解、运用数学基础知识和基本技能的升华过程.请同学们运用你所学的数学知识来研究和解决以下问题吧.
(1)探究:已知![]() 是平面上一个运动的点,若
是平面上一个运动的点,若![]() ,
,![]() ,则当点
,则当点![]() 位于 时,线段
位于 时,线段![]() 的长最小,最小值为 ;若
的长最小,最小值为 ;若![]() ,
,![]() ,则当点
,则当点![]() 位于 时,线段
位于 时,线段![]() 的长最小,最小值为 ;
的长最小,最小值为 ;
(2)应用:已知![]() 是一运动的点,
是一运动的点,![]() ,
,![]() ,如图①所示,分别以
,如图①所示,分别以![]() 为边作等腰直角三角形
为边作等腰直角三角形![]() 和等腰直角三角形
和等腰直角三角形![]() ,且
,且![]() ,连接
,连接![]() 和
和![]() .
.
①在图中找出与![]() 相等的线段,并说明理由;
相等的线段,并说明理由;
②何时线段![]() 可以取得最小值?请直接写出线段
可以取得最小值?请直接写出线段![]() 的最小值;
的最小值;
(3)拓展:如图②,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为矩形
为矩形![]() 对角线的交点,
对角线的交点,![]() 为
为![]() 边上任意一点,连接
边上任意一点,连接![]() 并延长与
并延长与![]() 边交于点
边交于点![]() ,现将图中
,现将图中![]() 与
与![]() 分别沿
分别沿![]() 与
与![]() 翻折,使点
翻折,使点![]() 与点
与点![]() 分别落在矩形
分别落在矩形![]() 内的点
内的点![]() ,
,![]() 处,连接
处,连接![]() ,则
,则![]() 的长有最小值吗?若有,请直接写出
的长有最小值吗?若有,请直接写出![]() 的长的最小值;若没有,请说明理由.
的长的最小值;若没有,请说明理由.
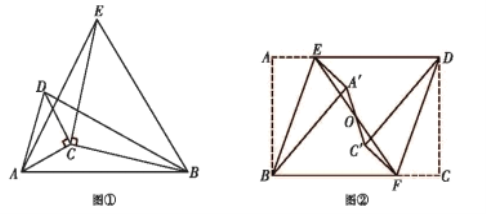
查看答案和解析>>
科目:初中数学 来源: 题型:
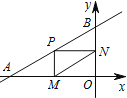
【题目】如图,直线![]() 与x轴、y轴分别交于A、B两点,点P是第二象限图象上一动点,PM⊥x轴于点M,PN⊥y轴于点N,连接MN,在点P的运动过程中,线段MN长度的最小值是________.
与x轴、y轴分别交于A、B两点,点P是第二象限图象上一动点,PM⊥x轴于点M,PN⊥y轴于点N,连接MN,在点P的运动过程中,线段MN长度的最小值是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com