
【题目】“综合与实践”是以问题为中心,以活动为平台,以解决某一实际的数学问题为目标,综合应用知识和方法解决问题,它是对数学知识的延伸和发展,是对理解、运用数学基础知识和基本技能的升华过程.请同学们运用你所学的数学知识来研究和解决以下问题吧.
(1)探究:已知![]() 是平面上一个运动的点,若
是平面上一个运动的点,若![]() ,
,![]() ,则当点
,则当点![]() 位于 时,线段
位于 时,线段![]() 的长最小,最小值为 ;若
的长最小,最小值为 ;若![]() ,
,![]() ,则当点
,则当点![]() 位于 时,线段
位于 时,线段![]() 的长最小,最小值为 ;
的长最小,最小值为 ;
(2)应用:已知![]() 是一运动的点,
是一运动的点,![]() ,
,![]() ,如图①所示,分别以
,如图①所示,分别以![]() 为边作等腰直角三角形
为边作等腰直角三角形![]() 和等腰直角三角形
和等腰直角三角形![]() ,且
,且![]() ,连接
,连接![]() 和
和![]() .
.
①在图中找出与![]() 相等的线段,并说明理由;
相等的线段,并说明理由;
②何时线段![]() 可以取得最小值?请直接写出线段
可以取得最小值?请直接写出线段![]() 的最小值;
的最小值;
(3)拓展:如图②,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为矩形
为矩形![]() 对角线的交点,
对角线的交点,![]() 为
为![]() 边上任意一点,连接
边上任意一点,连接![]() 并延长与
并延长与![]() 边交于点
边交于点![]() ,现将图中
,现将图中![]() 与
与![]() 分别沿
分别沿![]() 与
与![]() 翻折,使点
翻折,使点![]() 与点
与点![]() 分别落在矩形
分别落在矩形![]() 内的点
内的点![]() ,
,![]() 处,连接
处,连接![]() ,则
,则![]() 的长有最小值吗?若有,请直接写出
的长有最小值吗?若有,请直接写出![]() 的长的最小值;若没有,请说明理由.
的长的最小值;若没有,请说明理由.
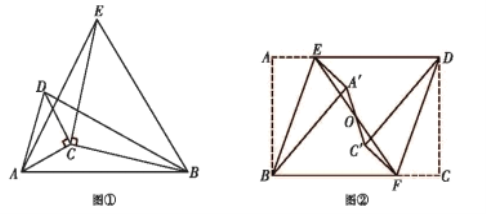
【答案】(1)线段![]() 上,2;线段
上,2;线段![]() 的延长线上,2;(2)①
的延长线上,2;(2)①![]() ,理由见详解;②当点C在AB上时,AE的值最小,最小值为
,理由见详解;②当点C在AB上时,AE的值最小,最小值为![]() ;(3)有最小值,最小值为
;(3)有最小值,最小值为![]() .
.
【解析】
(1)由题意可知,当点![]() 位于线段
位于线段![]() 上时有最小值,根据AB和PA的长确定点P是在线段
上时有最小值,根据AB和PA的长确定点P是在线段![]() 上还是在
上还是在![]() 的延长线上即可;
的延长线上即可;
(2)①证明![]() 全等即可找出与AD相等的线段;
全等即可找出与AD相等的线段;
②由(1)的结论,举一反三,即可找出AE取最小值的情况,再计算即可;
(3)根据前两问的启发,找到![]() 取最小值的情况,再推理计算即可.
取最小值的情况,再推理计算即可.
(1)由题意可得,当![]() ,
,![]() 时,当点
时,当点![]() 位于线段
位于线段![]() 上时,线段
上时,线段![]() 的长最小,最小值为2;
的长最小,最小值为2;
当![]() ,
,![]() 时,当点
时,当点![]() 位于线段
位于线段![]() 的延长线上时,线段
的延长线上时,线段![]() 的长最小,最小值为2;
的长最小,最小值为2;
(2)①![]()
理由:![]() 和
和![]() 是等腰直角三角形,
是等腰直角三角形,![]()
![]() ,
,![]()
![]()
![]()
![]() ;
;
②当点C在AB上时,AE的值最小,
此时C,D,E三点共线,CE⊥AB,
∴在Rt△ACE中,![]() ,
,
∵AB=3,AC=1,
∴BC=2,
∵![]() ,
,
∴CE=2,
∴![]() ,
,
∴最小值为![]() ;
;
(3)有最小值,
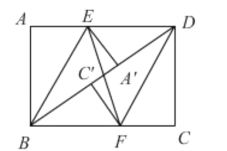
如图,要使![]() 最小,只有点
最小,只有点![]() ,
,![]() 落在矩形对角线BD上,
落在矩形对角线BD上,
矩形的对角线![]() ,
,
由对折可得![]() =BA=4,
=BA=4,
∴![]() =BD-
=BD-![]() =
=![]() -4,
-4,
∵四边形ABCD是矩形,且点![]() ,
,![]() 落在矩形对角线BD上,
落在矩形对角线BD上,
∴根据翻折的性质和矩形的性质可得,![]() =
=![]() ,∠
,∠![]() =∠
=∠![]() ,∠EDB=∠FBD,
,∠EDB=∠FBD,
∴△![]() ≌△
≌△![]() (AAS),
(AAS),
∴![]() =
=![]() ,
,
∴![]() =BD-
=BD-![]() -
-![]() =
=![]() -2(
-2(![]() -4)=
-4)=![]() ,
,
∴![]() 长的最小值为
长的最小值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,动点E从A出发,沿A→B→C方向运动,当点E到达点C时停止运动,过点E作EF⊥AE交CD于点F,设点E运动路程为x,CF=y,如图2所表示的是y与x的函数关系的大致图象,给出下列结论:①a=3;②当CF=![]() 时,点E的运动路程为
时,点E的运动路程为![]() 或
或![]() 或
或![]() ,则下列判断正确的是( )
,则下列判断正确的是( )
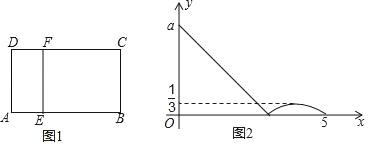
A. ①②都对 B. ①②都错 C. ①对②错 D. ①错②对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于![]() 的一元二次方程
的一元二次方程![]() 有两个实数根,且其中一根为另一根的2倍,则称这样的方程为“倍根方程”,以下关于倍根方程的说法,不正确的是( )
有两个实数根,且其中一根为另一根的2倍,则称这样的方程为“倍根方程”,以下关于倍根方程的说法,不正确的是( )
A.方程![]() 是倍根方程;
是倍根方程;
B.若![]() 是倍根方程,则
是倍根方程,则![]() ;
;
C.若方程![]() 是倍根方程,且相异两点
是倍根方程,且相异两点![]() 都在抛物线
都在抛物线![]() 上,则方程
上,则方程![]() 的一个根为
的一个根为![]() ;
;
D.若点![]() 在反比例函数
在反比例函数![]() 的图象上,则关于
的图象上,则关于![]() 的方程
的方程![]() 是倍根方程.
是倍根方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“自主互助学习型课堂竞赛”中,为奖励表现突出的同学,初一(7)班利用班费![]() 元钱,购买钢笔、相册、笔记本三种奖品,其中钢笔至多买
元钱,购买钢笔、相册、笔记本三种奖品,其中钢笔至多买![]() 支,若钢笔每支
支,若钢笔每支![]() 元,相册每本
元,相册每本![]() 元,笔记本每本
元,笔记本每本![]() 元,在把钱都用尽的条件下,买法共有( )
元,在把钱都用尽的条件下,买法共有( )
A.![]() 种B.
种B.![]() 种C.
种C.![]() 种D.
种D.![]() 种
种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行团32人在景区A游玩,他们由成人、少年和儿童组成.已知儿童10人,成人比少年多12人.
(1)求该旅行团中成人与少年分别是多少人?
(2)因时间充裕,该团准备让成人和少年(至少各1名)带领10名儿童去另一景区B游玩.景区B的门票价格为100元/张,成人全票,少年8折,儿童6折,一名成人可以免费携带一名儿童.
①若由成人8人和少年5人带队,则所需门票的总费用是多少元?
②若剩余经费只有1200元可用于购票,在不超额的前提下,最多可以安排成人和少年共多少人带队?求所有满足条件的方案,并指出哪种方案购票费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,以AB为直径的⊙O交BC于点D,交AC于点F,过点C作CE∥AB,且∠CAD=∠CAE.
(1)求证:AE是⊙O的切线;
(2)若AB=8,AC=6,求CE的长.
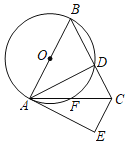
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解“停课不停学”过程中学生对网课内容的喜爱程度,某校开展了一次网上问卷调查.随机抽取部分学生,按四个类别统计,其中A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”,并将调查结果绘制成下面两幅不完整的统计图.
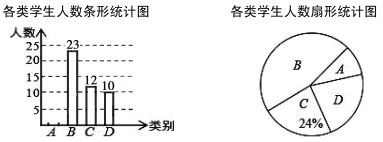
请根据图中提供的信息,解决下列问题:
(1)这次共抽取 名学生进行统计调查,扇形统计图中D类所在扇形的圆心角度数为 ;
(2) 将条形统计图补充完整;
(3) 若该校共有3000名学生,估计该校表示“喜欢”的B类学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市教委为了让广大青少年学生走向操场、走进自然、走到阳光下,积极参加体育锻炼,启动了“学生阳光体育运动”,其中有一项是短跑运动,短跑运动可以锻炼人的灵活性,增强人的爆发力,因此张明和李亮在课外活动中报名参加了百米训练小组.在近几次百米训练中,教练对他们两人的测试成绩进行了统计和分析,请根据图表中的信息解答以下问题:
成绩统计分析表
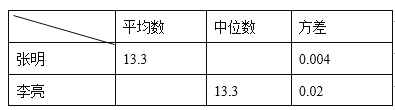
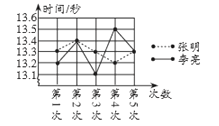
(1)张明第2次的成绩为__________秒;
(2)请补充完整上面的成绩统计分析表;
(3)现在从张明和李亮中选择一名成绩优秀的去参加比赛,若你是他们的教练,应该选择谁? 请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com