
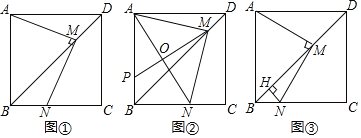
【题目】如图,在正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上的一个动点
上的一个动点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
(1)如图①,求证:![]() ;
;
(2)如图②,连接![]() 为
为![]() 的中点,
的中点,![]() 的延长线交边
的延长线交边![]() 于点
于点![]() ,当
,当![]() 时,求
时,求![]() 和
和![]() 的长;
的长;
(3)如图③,过点![]() 作
作![]() 于
于![]() ,当
,当![]() 时,求
时,求![]() 的面积.
的面积.
【答案】(1)见解析;(2)![]() ;
;![]() ;(3)面积为
;(3)面积为![]() .
.
【解析】
(1)过点M作MF⊥AB于F,作MG⊥BC于G,由正方形的性质得出∠ABD=∠DBC=45°,由角平分线的性质得出MF=MG,证得四边形FBGM是正方形,得出∠FMG=90°,证出∠AMF=∠NMG,证明△AMF≌△NMG,即可得出结论;
(2)证明Rt△AMN∽Rt△BCD,得出 ,求出AN=2
,求出AN=2![]() ,由勾股定理得出BN=
,由勾股定理得出BN=![]() =4,由直角三角形的性质得出OM=OA=ON=
=4,由直角三角形的性质得出OM=OA=ON=![]() AN=
AN=![]() ,OM⊥AN,证明△PAO∽△NAB,得出
,OM⊥AN,证明△PAO∽△NAB,得出![]() ,求出OP=
,求出OP=![]() ,即可得出结果;
,即可得出结果;
(3)过点A作AF⊥BD于F,证明△AFM≌△MHN得出AF=MH,求出AF=![]() BD=
BD=![]() ×6
×6![]() =3
=3![]() ,得出MH=3
,得出MH=3![]() ,MN=2
,MN=2![]() ,由勾股定理得出HN=
,由勾股定理得出HN=![]() ,由三角形面积公式即可得出结果.
,由三角形面积公式即可得出结果.
(1)证明:过点![]() 作
作![]() 于
于![]() ,作
,作![]() 于
于![]() ,如图①所示:
,如图①所示:

![]() ,
,
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中, 
![]() ,
,
![]() ;
;
(2)解:在![]() 中,由(1)知:
中,由(1)知:![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,

在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
解得:![]() ,
,
![]() 在
在![]() 中,
中,![]() ,
,
![]() 在
在![]() 中,
中,![]() 是
是![]() 的中点,
的中点,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,即:
,即: ![]() ,
,
解得:![]() ,
,
![]() ;
;
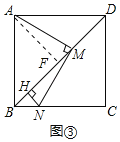
(3)解:过点![]() 作
作![]() 于
于![]() ,如图③所示:
,如图③所示:
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,

![]() ,
,
![]() ,
,
在等腰直角![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]() 的面积为
的面积为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图:是长方形纸片ABCD折叠的情况,纸片的宽度AB=8cm,长AD=10cm,AD沿点A对折,点D正好落在BC上的M处,AE是折痕.
(1)求CM的长;
(2)求梯形ABCE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
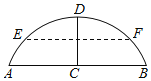
【题目】如图,有一拱桥的桥拱是圆弧形,已知桥拱的水面跨度AB(弧所对的弦的长)为8米,拱高CD(弧的中点到弦的距离)为2米.
(1)求桥拱所在圆的半径长;
(2)如果水面AB上升到EF时,从点E测得桥顶D的仰角为α,且cotα=3,求水面上升的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中(如图),已知函数
中(如图),已知函数![]() 的图像和反比例函数的在第一象限交于A点,其中点A的横坐标是1.
的图像和反比例函数的在第一象限交于A点,其中点A的横坐标是1.
(1)求反比例函数的解析式;
(2)把直线![]() 平移后与
平移后与![]() 轴相交于点B,且
轴相交于点B,且![]() ,求平移后直线的解析式.
,求平移后直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
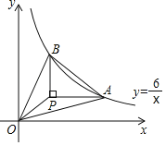
【题目】如图,A、B是函数y=![]() 上两点,P为一动点,作PB∥y轴,PA∥x轴,下列说法:①△AOP≌△BOP;②S△AOP=S△BOP;③若OA=OB,则OP平分∠AOB;④若S△BOP=2,则S△ABP=4,正确有____(填序号)
上两点,P为一动点,作PB∥y轴,PA∥x轴,下列说法:①△AOP≌△BOP;②S△AOP=S△BOP;③若OA=OB,则OP平分∠AOB;④若S△BOP=2,则S△ABP=4,正确有____(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为192m2, 求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:![]() ,
,![]() ,
,![]() ,将以上三个等式两边分别相加得:
,将以上三个等式两边分别相加得:![]() .
.
(1)观察发现
![]() _________;
_________;
![]() __________.
__________.
(2)初步应用
利用(1)的结论,解决下列问题:
①把![]() 拆成两个分子为1的正的真分数之差,即
拆成两个分子为1的正的真分数之差,即![]() __________;
__________;
②把![]() 拆成两个分子为1的正的真分数之和,即
拆成两个分子为1的正的真分数之和,即![]() __________.
__________.
(3)深入探究
定义“◆”是一种新的运算,若![]() ,
,![]() ,
,![]() ,则
,则![]() 计算的结果是_________.
计算的结果是_________.
(4)拓展延伸
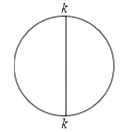
第一次用一条直径将圆周分成两个半圆(如图),在每个分点标上质数![]() ,记2个数的和为
,记2个数的和为![]() ,第二次将两个半圆都分成
,第二次将两个半圆都分成![]() 圆,在新产生的分点标相邻的已标的两个数的和的
圆,在新产生的分点标相邻的已标的两个数的和的![]() ,记4个数的和为
,记4个数的和为![]() ;第三次将四个
;第三次将四个![]() 圆分成
圆分成![]() 圆,在新产生的分点标相邻的已标的两个数的和的
圆,在新产生的分点标相邻的已标的两个数的和的![]() ,记8个数的和为
,记8个数的和为![]() ;第四次将八个
;第四次将八个![]() 圆分成
圆分成![]() 圆,在新产生的分点标相邻的已标的两个数的和的
圆,在新产生的分点标相邻的已标的两个数的和的![]() ,记16个数的和为
,记16个数的和为![]() ;……如此进行了
;……如此进行了![]() 次.
次.
①![]() _________(用含
_________(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
②![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位计划购进![]() 三种型号的礼品共
三种型号的礼品共![]() 件,其中
件,其中![]() 型号礼品
型号礼品![]() 件,
件,![]() 型号礼品比
型号礼品比![]() 型号礼品多
型号礼品多![]() 件.已知三种型号礼品的单价如下表:
件.已知三种型号礼品的单价如下表:
型号 |
|
|
|
单价(元/件) |
|
|
|
(1)求计划购进![]() 和
和![]() 两种型号礼品分别多少件?
两种型号礼品分别多少件?
(2)实际购买时,厂家给予打折优惠销售(如: ![]() 折指原价
折指原价![]() ,在计划总价额不变的情况下,准备购进这批礼品.
,在计划总价额不变的情况下,准备购进这批礼品.
①若只购进![]() 两种型号礼品,且
两种型号礼品,且![]() 型礼品件数不超过
型礼品件数不超过![]() 型礼品的
型礼品的![]() 倍,求
倍,求![]() 型礼品最多购进多少件?
型礼品最多购进多少件?
②若只购进![]() 两种型号礼品,它们的单价分别打
两种型号礼品,它们的单价分别打![]() 折、
折、![]() 折,
折,![]() 均为整数,且购进的礼品总数比计划多
均为整数,且购进的礼品总数比计划多![]() 件,求
件,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
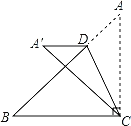
【题目】如图,在Rt△ABC中BC=AC=4,D是斜边AB上的一个动点,把△ACD沿直线CD折叠,点A落在同一平面内的A′处,当A′D垂直于Rt△ABC的直角边时,AD的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com