
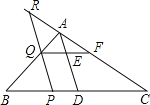
【题目】已知三角形ABC,AD为BC边中线,P为BC上一动点,过点P作AD的平行线,交直线AB或延长线于点Q,交CA或延长线于点R.
(1)当点P在BD上运动时,过点Q作BC的平行线交AD于E点,交AC于F点,求证:QE=EF;
(2)当点P在BC上运动时,求证:PQ+PR为定值.
【答案】(1)证明见解析;(2)证明见解析
【解析】
(1)根据平行线QF∥BC,可以推知△AQE∽△ABD,△AEF∽△ADC;然后根据相似三角形的对应边成比例可求得![]() ;再根据已知条件“AD为BC边中线”来证明QE=EF;
;再根据已知条件“AD为BC边中线”来证明QE=EF;
(2)分类讨论:
①当点P与点B(或点C)重合时,AD为△B(P)RC(或△C(P)BQ)的中位线,PQ+PR=2AD;
②当点P在BD上(不与点B重合)运动时,由(1)证明可知,AE为△RQF的中位线,PQ+PR=2AD;
③当点P在CD上(不与点C重合)运动时,PQ+PR=2AD.
(1)证明:∵QF∥BC,
∴△AQE∽△ABD,△AEF∽△ADC.
∴![]() ,
,
∵BD=DC,
∴QE=EF.
(2)解:当点P与点B(或点C)重合时,AD为△B(P)RC(或△C(P)BQ)的中位线,
∴PQ+PR=2AD.
当点P在BD上(不与点B重合)运动时,由(1)证明可知,AE为△RQF的中位线,
∴RQ=2AE.
∵QF∥BC,PQ∥AD,
∴四边形PQED为平行四边形.
∴PQ=DE,
∴PQ+PR=2DE+QR=2DE+2AE=2AD.
同理可证,当点P在CD上(不与点C重合)运动时,
PQ+PR=2AD.
∴P在BC上运动时,PQ+PR为定值,
即PQ+PR=2AD.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中(如图),已知函数
中(如图),已知函数![]() 的图像和反比例函数的在第一象限交于A点,其中点A的横坐标是1.
的图像和反比例函数的在第一象限交于A点,其中点A的横坐标是1.
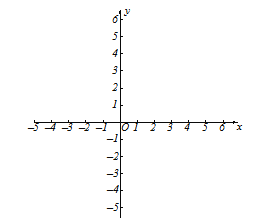
(1)求反比例函数的解析式;
(2)把直线![]() 平移后与
平移后与![]() 轴相交于点B,且
轴相交于点B,且![]() ,求平移后直线的解析式.
,求平移后直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位计划购进![]() 三种型号的礼品共
三种型号的礼品共![]() 件,其中
件,其中![]() 型号礼品
型号礼品![]() 件,
件,![]() 型号礼品比
型号礼品比![]() 型号礼品多
型号礼品多![]() 件.已知三种型号礼品的单价如下表:
件.已知三种型号礼品的单价如下表:
型号 |
|
|
|
单价(元/件) |
|
|
|
(1)求计划购进![]() 和
和![]() 两种型号礼品分别多少件?
两种型号礼品分别多少件?
(2)实际购买时,厂家给予打折优惠销售(如: ![]() 折指原价
折指原价![]() ,在计划总价额不变的情况下,准备购进这批礼品.
,在计划总价额不变的情况下,准备购进这批礼品.
①若只购进![]() 两种型号礼品,且
两种型号礼品,且![]() 型礼品件数不超过
型礼品件数不超过![]() 型礼品的
型礼品的![]() 倍,求
倍,求![]() 型礼品最多购进多少件?
型礼品最多购进多少件?
②若只购进![]() 两种型号礼品,它们的单价分别打
两种型号礼品,它们的单价分别打![]() 折、
折、![]() 折,
折,![]() 均为整数,且购进的礼品总数比计划多
均为整数,且购进的礼品总数比计划多![]() 件,求
件,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是半圆O的直径,AB=6,点C在半圆O上.过点A作AD⊥OC,垂足为点D,AD的延长线与弦BC交于点E,与半圆O交于点F(点F不与点B重合).
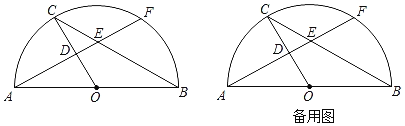
(1)当点F为![]() 的中点时,求弦BC的长;
的中点时,求弦BC的长;
(2)设OD=x,![]() =y,求y与x的函数关系式;
=y,求y与x的函数关系式;
(3)当△AOD与△CDE相似时,求线段OD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
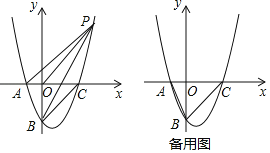
【题目】已知抛物线y=![]() x2+bx+c经过点A(﹣2,0),B(0、﹣4)与x轴交于另一点C,连接BC.
x2+bx+c经过点A(﹣2,0),B(0、﹣4)与x轴交于另一点C,连接BC.
(1)求抛物线的解析式;
(2)如图,P是第一象限内抛物线上一点,且S△PBO=S△PBC,求证:AP∥BC;
(3)在抛物线上是否存在点D,直线BD交x轴于点E,使△ABE与以A,B,C,E中的三点为顶点的三角形相似(不重合)?若存在,请求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
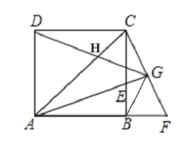
【题目】如图,ABCD为正方形,∠CAB的角平分线交BC于点E,过点C作CF⊥AE交AE的延长线于点G,CF与AB的延长线交于点F,连接BG、DG、与AC相交于点H,则下列结论:①![]() ABE
ABE![]()
![]() CBF;②GF=CG;③BG⊥DG;④
CBF;②GF=CG;③BG⊥DG;④![]() ,其中正确的是______.
,其中正确的是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
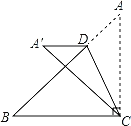
【题目】如图,在Rt△ABC中BC=AC=4,D是斜边AB上的一个动点,把△ACD沿直线CD折叠,点A落在同一平面内的A′处,当A′D垂直于Rt△ABC的直角边时,AD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十八大以来,某校已举办五届校园艺术节.为了弘扬中华优秀传统文化,每届艺术节上都有一些班级表演“经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”等节目.小颖对每届艺术节表演这些节目的班级数进行统计,并绘制了如图所示不完整的折线统计图和扇形统计图.
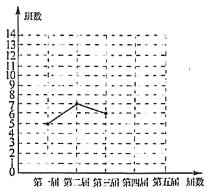
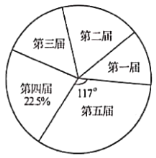
(1)五届艺术节共有________个班级表演这些节日,班数的中位数为________,在扇形统计图中,第四届班级数的扇形圆心角的度数为________;
(2)补全折线统计图;
(3)第六届艺术节,某班决定从这四项艺术形式中任选两项表演(“经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”分别用![]() ,
,![]() ,
,![]() ,
,![]() 表示).利用树状图或表格求出该班选择
表示).利用树状图或表格求出该班选择![]() 和
和![]() 两项的概率.
两项的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC的重心为G,△DEF与△ABC关于点G成中心对称,将它们重叠部分的面积记作S1,△ABC的面积记作S2,那么![]() 的值是_____
的值是_____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com