
【题目】已知抛物线![]()
(1)证明:不论m为何值,抛物线图象的顶点![]() 均在某一直线
均在某一直线![]() 的图象上,求此直线
的图象上,求此直线![]() 的函数解析式;
的函数解析式;
(2)当![]() 时,点P为抛物线上一点,且
时,点P为抛物线上一点,且![]() ,求点P的坐标;
,求点P的坐标;
(3)将(2)中的抛物线![]() 沿x轴翻折再向上平移1个单位向右平移
沿x轴翻折再向上平移1个单位向右平移![]() 个单位得抛物线
个单位得抛物线![]() ,设抛物线
,设抛物线![]() 的顶点为
的顶点为![]() ,抛物线
,抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() (A在B的左边),且
(A在B的左边),且![]() ∥
∥![]() ,求
,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]() (3)
(3)![]()
【解析】试题分析:(1)利用配方法可确定抛物线的顶点M坐标为(m-1,-m-2),然后令x=m-1,y=-m-2,然后消去m得到x和y的关系式即可;
(2)先确定抛物线解析式为y=x2-2x-3,点M的坐标为(1,-4),利用旋转的定义,将线段OM绕点O逆时针旋转90°得线段OC,与抛物线相交于点P,如图1,从而得到点C坐标,再求出直线OP的解析式为y=![]() x,然后解方程组
x,然后解方程组 得P点坐标;
得P点坐标;
(3)利用抛物线的几何变换得到N(n+1,5),抛物线C2的解析式为y=-(x-n-1)2+5,过点M作ME⊥x轴于点E,过点N作NF⊥x轴于点F,如图2,根据抛物线与x轴的交点问题求出A点和B点坐标,然后证明Rt△AME∽Rt△BNF,再利用相似比得到关于n的方程,解方程可得到n的值.
试题解析:(1)证明:y=x2-2(m-1)x+m2-3m-1=[x-(m-1)]2-m-2,则抛物线的顶点M坐标为(m-1,-m-2),
令x=m-1,y=-m-2,
则x+y=-3,
所以直线l的函数解析式为y=-x-3;
(2)当m=2时,抛物线解析式为y=x2-2x-3,点M的坐标为(1,-4),
将线段OM绕点O逆时针旋转90°得线段OC,与抛物线相交于点P,如图1,

则点C坐标为(4,1),设直线OC的解析式为y=kx,
把C(4,1)代入得4k=1,解得k=![]() ,
,
所以直线OP的解析式为y=![]() x,
x,
解方程组 得
得 或
或 ,
,
所以点P的坐标为(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() );
);
(3)由题意可知,抛物线C2的顶点N(n+1,5),则抛物线C2的解析式为y=-(x-n-1)2+5,
过点M作ME⊥x轴于点E,过点N作NF⊥x轴于点F,如图2,

当y=0时,-(x-n-1)2+5=0,解得x1=n+1-![]() ,x2=n+1+
,x2=n+1+![]() ,
,
∴A(n+1-![]() ,0),B(n+1+
,0),B(n+1+![]() ,0),
,0),
∵AM∥BN,
∴∠MAE=∠NBF,
∴Rt△AME∽Rt△BNF,
∴![]() ,即
,即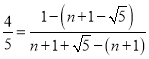 ,
,
∴n=![]() .
.


科目:初中数学 来源: 题型:
【题目】探究:如图①,在ABCD中,AC,BD交于点O,过点O的直线交AD于E,交BC于F.
(1)求证:OE=OF.
(2)求证:四边形AEFB与四边形DEFC的周长相等;
(3)直线EF是否将ABCD的面积二等分?
应用:张大爷家有一块平行四边形的菜园,园中有一口水井P,如图②所示,张大爷计划把菜园平均分成两块,分别种植西红柿和茄子,且使两块地共用这口水井,请你帮助张大爷把地分开.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师家距学校1 900 m,某天他步行去上班,走到路程的一半时发现忘带手机,此时离上班时间还有23 min,于是他立刻步行回家取手机,随后骑电瓶车返回学校.已知李老师骑电瓶车到学校比他步行到学校少用20 min,且骑电瓶车的平均速度是步行平均速度的5倍,李老师到家开门、取手机、启动电瓶车等共用4 min.
(1)求李老师步行的平均速度;
(2)请你判断李老师能否按时上班,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有20道竞赛题,对于每道题,答对得6分,答错或不答扣3分.小明在这次竞赛中的得分不少于80分,但又不多于90分,则小明答对的题数是( )道.
A.14
B.15
C.16
D.17
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要了解全校学生的课外作业负担情况,你认为以下抽样方法中比较合理的是( )
A.调查九年级全体学生
B.调查七、八、九年级各30名学生
C.调查全体女生
D.调查全体男生
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 轴于点
轴于点![]() ,
, ![]() ,反比例函数
,反比例函数![]() 与OA、AB分别相交于点D、C,且点D为OA的中点,
与OA、AB分别相交于点D、C,且点D为OA的中点,
(1)求反比例函数的解析式
(2)过点B的直线![]() 与反比例函数
与反比例函数![]() 图象交于第三象限内一点F,求四边形
图象交于第三象限内一点F,求四边形![]() 的面积
的面积

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=10,BC=3,E为AB边的中点,P为CD边上的点,且△AEP是腰长为5的等腰三角形,则DP=_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,对角线AC上有一点P,连接BP、DP,过点P作PE⊥PB交CD于点E,连接BE.
(1)求证:BP=EP;
(2)若CE=3,BE=6,求∠CPE的度数;
(3)探究AP、PC、BE之间的数量关系,并给予证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com