
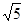 cm,且tan∠EFC=
cm,且tan∠EFC= .
.
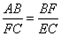 即:
即: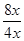 =
=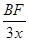 ∴BF=6x ∴BC="BF-CF=6x+" 4x= 10x
∴BF=6x ∴BC="BF-CF=6x+" 4x= 10x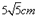 ,则有
,则有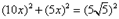
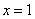 (
(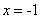 舍去) ∴AB+BC+CD+DA=36x=36(cm) 答:矩形ABCD的周长为36cm.
舍去) ∴AB+BC+CD+DA=36x=36(cm) 答:矩形ABCD的周长为36cm. ,可得
,可得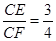 ,则可设CE=3k,则CF=4k,由勾股定理得EF=DE=5k.继而求得BF与BC,则可求得k的值,由矩形ABCD的周长=2(AB+BC)求得结果.
,则可设CE=3k,则CF=4k,由勾股定理得EF=DE=5k.继而求得BF与BC,则可求得k的值,由矩形ABCD的周长=2(AB+BC)求得结果.

 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源:不详 题型:单选题
| A.①,② | B.①,②,③ | C.②,③,④ | D.①,②,③,④ |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
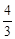 ,④
,④ 中,正确的有【 】
中,正确的有【 】
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 = .
= .查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题


 < S△OQB,若存在,求出t的取值范围,若不存在,试说明理由。
< S△OQB,若存在,求出t的取值范围,若不存在,试说明理由。 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com