
 如图,在平面直角坐标系中,O为坐标原点,点N的坐标为(20,0),点M在第一象限内,且OM=10,sin∠MON=$\frac{3}{5}$.求:
如图,在平面直角坐标系中,O为坐标原点,点N的坐标为(20,0),点M在第一象限内,且OM=10,sin∠MON=$\frac{3}{5}$.求:分析 (1)过点M作MP⊥ON,垂足为点P,根据已知条件得到MP=6,由勾股定理得到OP=$\sqrt{{{10}^2}-{6^2}}=8$,于是得到点M的坐标是(8,6);
(2)由(1),知MP=6,PN=20-8=12,根据勾股定理得到MN=$\sqrt{{6}^{2}+1{2}^{2}}$=6$\sqrt{5}$,于是得到结论.
解答 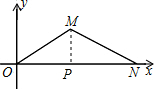 解:(1)过点M作MP⊥ON,垂足为点P,
解:(1)过点M作MP⊥ON,垂足为点P,
在Rt△MOP中,由sin∠MON=$\frac{3}{5}$,OM=10,
得$\frac{MP}{10}=\frac{3}{5}$,
即MP=6,由
勾股定理,得OP=$\sqrt{{{10}^2}-{6^2}}=8$,
∴点M的坐标是(8,6);
(2)由(1),知MP=6,PN=20-8=12,
∴MN=$\sqrt{{6}^{2}+1{2}^{2}}$=6$\sqrt{5}$,
∴cos∠MNO=$\frac{PN}{MN}=\frac{12}{{6\sqrt{5}}}=\frac{{2\sqrt{5}}}{5}$.
点评 本题考查了解直角三角形,坐标于图形的性质,正确的作出辅助线是解题的关键.


 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
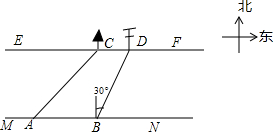 在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度.(结果保留根号)
在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com