
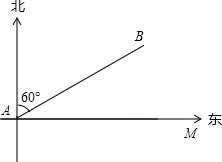
 一艘船自西向东航行,在A得到消息,在其北偏东60°方向,距离20海里的B点,测得有一暗礁群在以点B为圆心,10$\sqrt{2}$海里为半径的圆内,问如果轮船继续沿正东方向航行有无触礁的危险?如果有危险,轮船至少要偏离原来航线多少度,才能保证航线的安全?
一艘船自西向东航行,在A得到消息,在其北偏东60°方向,距离20海里的B点,测得有一暗礁群在以点B为圆心,10$\sqrt{2}$海里为半径的圆内,问如果轮船继续沿正东方向航行有无触礁的危险?如果有危险,轮船至少要偏离原来航线多少度,才能保证航线的安全? 分析 过B作BC⊥AM于C,则BC的长是A沿AM方向距离B点的最短距离,求出BC长和10$\sqrt{2}$比较可得出轮船继续沿正东方向航行有无触礁的危险;设安全航向为AN,作BD⊥AN于点D,解Rt△BAD,求出∠BAD=45°,则∠CAN=∠BAD-∠BAC=15°.
解答 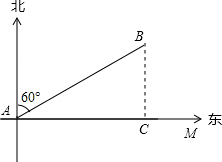 解:过B作BC⊥AM于C,则∠BCA=90°,且BC的长是A沿AM方向距离B点的最短距离.
解:过B作BC⊥AM于C,则∠BCA=90°,且BC的长是A沿AM方向距离B点的最短距离.
在Rt△ABC中,
∵∠BCA=90°,∠BAC=90°-60°=30°,AB=20海里,
∴BC=$\frac{1}{2}$AB=10海里<10$\sqrt{2}$海里,
∴轮船继续向正东方向航行,有触礁的危险;
为了安全,应改变航行方向,并且保证点B到航线的距离不小于暗礁的半径10$\sqrt{2}$海里,
即这个距离至少为10$\sqrt{2}$海里,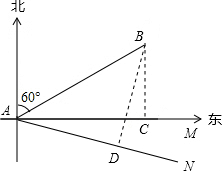 设安全航向为AN,作BD⊥AN于点D,
设安全航向为AN,作BD⊥AN于点D,
在Rt△BAD中,∵AB=20海里,BD=10$\sqrt{2}$海里,
∴sin∠BAD=$\frac{BD}{AB}$=$\frac{10\sqrt{2}}{20}$=$\frac{\sqrt{2}}{2}$,
∴∠BAD=45°,
∴∠CAN=∠BAD-∠BAC=45°-30°=15°.
答:轮船自A处开始至少沿东偏南15°度方向航行,才能安全通过这一海域.
点评 本题考查了解直角三角形的应用-方向角问题,关键是如何构造直角三角形并知道求哪一条线段的长,题目比较典型,是一道比较好的题目.


科目:初中数学 来源: 题型:选择题
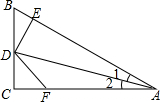 如图,DC⊥AC于C,DE⊥AB于E,并且DE=DC,则下列结论中正确的是( )
如图,DC⊥AC于C,DE⊥AB于E,并且DE=DC,则下列结论中正确的是( )| A. | ∠1=∠2 | B. | DE=DF | C. | BD=FD | D. | AB=AC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 如果两个角相等,那么这两个角一定是对顶角 | |
| B. | 两个互补的角一定是邻补角 | |
| C. | 如果a2=b2,那么a=b | |
| D. | 如果两个角是对顶角,那么这两个角一定相等 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com