
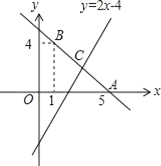
【题目】如图,已知一条直线经过点A(5,0)、B(1,4).
(1)求直线AB的解析式;
(2)若直线y=2x﹣4与直线AB相交于点C,请问直线y=﹣![]() x+4是否也经过点C?
x+4是否也经过点C?
科目:初中数学 来源: 题型:
【题目】一队卡车运一批货物,若每辆卡车装7吨货物,则剩余10吨货物装不完;若每辆卡车装8吨货物,则最后一辆卡车只装3吨货物就装完了这批货物,那么这批货物共有吨.
查看答案和解析>>
科目:初中数学 来源: 题型:
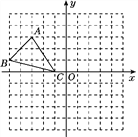
【题目】如图,已知网格上最小的正方形的边长为1.
(1)分别写出A,B,C三点的坐标;
(2)作△ABC关于y轴的对称图形△A′B′C′(不写作法),想一想:关于y轴对称的两个点之间有什么关系?
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
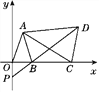
【题目】如图,在平面直角坐标系中,已知点A(a-1,a+b),B(a,0),且|a+b-3|+(a-2b)2=0,C为x轴上点B右侧的动点,以AC为腰作等腰三角形ACD,使AD=AC,∠CAD=∠OAB,直线DB交y轴于点P.
(1)求证:AO=AB;
(2)求证:△AOC≌△ABD;
(3)当点C运动时,点P在y轴上的位置是否发生改变,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:点O是∠EPF的平分线上的一点,以点O为圆心的圆与角的两边分别交于点A、B和C、D。
(1)求证:![]() =
=![]() ;
;
(2)若角的顶点P在圆内,上述结论还成立吗?若不成立,请说明理由;若成立,请加以证明。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明设计了点做圆周运动的一个动画游戏,如上图所示,甲、乙两点分别从直径的两端点A、B以顺时针、逆时针的方向同时沿圆周运动,甲运动的路程l(cm)与时间t(s)满足关系:l=![]() t2+
t2+![]() t(t≥0),乙以4cm/s的速度匀速运动,半圆的长度为21cm.
t(t≥0),乙以4cm/s的速度匀速运动,半圆的长度为21cm.
(1)甲运动4s后的路程是多少?
(2)甲、乙从开始运动到第一次相遇时,它们运动了多少时间?
(3)甲、乙从开始运动到第二次相遇时,它们运动了多少时间?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“夕阳红”养老院共有普通床位和高档床位共500张.已知今年一月份入住普通床位老人300人,入住高档床位老人90人,共计收费51万元;今年二月份入住普通床位老人350人,入住高档床位老人100人,共计收费58万元.
(1)求普通床位和高档床位每月收费各多少元?
(2)根据国家养老政策规定,为保障普通居民的养老权益,所有实际入住高档床位数不得超过实际入住普通床位数的三分之一;另外为扶持养老企业发展国家民政局财政对每张入住的床位平均每年都是给予养老院企业2400元的补贴.经测算,该养老院普通床位的运营成本是每月1200元/张,入住率为90%;高档床位的运营成本是每月2000元/张,入住率为70%.问该养老院应该怎样安排500张床的普通床位和高档床位数量,才能使每月的利润最大,最大为多少元?(月利润=月收费-月成本+月补贴)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com