
����Ŀ����Ϧ���족����Ժ������ͨ��λ�ߵ���λ��500�ţ���֪����һ�·���ס��ͨ��λ����300�ˣ���ס�ߵ���λ����90�ˣ������շ�51��Ԫ��������·���ס��ͨ��λ����350�ˣ���ס�ߵ���λ����100�ˣ������շ�58��Ԫ��
��1������ͨ��λ�ߵ���λÿ���շѸ�����Ԫ��
��2�����ݹ����������߹涨��Ϊ������ͨ���������Ȩ�棬����ʵ����ס�ߵ���λ�����ó���ʵ����ס��ͨ��λ��������֮һ������Ϊ����������ҵ��չ���������ֲ�����ÿ����ס�Ĵ�λƽ��ÿ�궼�Ǹ�������Ժ��ҵ2400Ԫ�IJ����������㣬������Ժ��ͨ��λ����Ӫ�ɱ���ÿ��1200Ԫ/�ţ���ס��Ϊ90%���ߵ���λ����Ӫ�ɱ���ÿ��2000Ԫ/�ţ���ס��Ϊ70%���ʸ�����ԺӦ����������500�Ŵ�����ͨ��λ�ߵ���λ����������ʹÿ�µ�����������Ϊ����Ԫ����������=���շ�-�³ɱ�+�²�����
���𰸡���1����ͨ��λ���շ�Ϊ800Ԫ���ߵ���λ���շ�Ϊ3000Ԫ��
��2���ð�����ͨ��λ350�š��ߵ���λ150�ţ�����ʹÿ�µ�����������Ϊ63000Ԫ.
�������������������1������ͨ��λ�ߵ���λÿ���շ�Ϊx��yԪ�����������г��������ɣ�
��2���谲����ͨ��λa�ţ����������г�����ʽ��ɣ�
���������
�⣺��1������ͨ��λ���շ�ΪxԪ���ߵ���λ���շ�ΪyԪ��
��������ã� ![]()
��֮�ã� ![]()
����ͨ��λ���շ�Ϊ800Ԫ���ߵ���λ���շ�Ϊ3000Ԫ��
��2���裺Ӧ������ͨ��λa�ţ���ߵ���λΪ��500��a���ţ�
�����⣺0.7��(500��a)��0.9��![]() a
a
��֮�ã� a��350
ÿ�Ŵ�λ��ƽ��������2400��12��200Ԫ
���������ܶ�Ϊw����������ã�
w=90%��800a+70%��3000(500��a)��90%��1200a��70%��2000(500��a)+200a��90%+200(500��a)��70% = ��1020a+420000
��k����1020<0
��w����a���������С
�൱a��350ʱ��w�����ֵ�� ��1020��350+420000��63000
��Ӧ�ð�����ͨ��λ350�š��ߵ���λ150�ţ�����ʹÿ�µ�����������Ϊ63000Ԫ�������ߵ���λ����Ӧ��������֣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
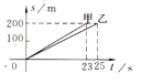
����Ŀ����ͼ��ʾ���Ǽס�������������ھ��еı���ͼ������t��ʾ����ʱ����ʱ�䣬s��ʾ���ܵľ��룬����ͼ��ش��������⣺
(1)ͼ��ӳ������������֮��Ĺ�ϵ?
(2)���ǽ��е��Ƕ�Զ�ı���?
(3)˭�ǹھ�?
(4)������α����е��ٶ��Ƕ���?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��EOF��������E��O��F�䣬ʹ�á�E��O��F������EOF���������ĺ���˳���ǡ� ��
���Ե�C��ΪԲ�ģ���CD�ij�Ϊ�뾶��������ǰ��Ļ��ڵ�D�䣻���Ե�OΪԲ�ģ������ⳤΪ�뾶��������OE�ڵ�C����OF�ڵ�D����������O��E�䣻���Ե�O��ΪԲ�ģ���OC�ij�Ϊ�뾶��������O��E���ڵ�C�䣻�ݹ���D��������O��F������E��O��F������������Ľ�.
A. �ۢڢ٢ܢ� B. �ۢڢܢ٢�
C. �ڢܢۢ٢� D. �ڢۢ٢ܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������������A��B��C���������¶��壺������ε��κ�һ���߾���ij��������ƽ�У���A��B��C���㶼�ھ��ε��ڲ���߽��ϣ���Ƹþ���Ϊ��A��B��C�ĸ��Ǿ��Σ���A��B��C�����и��Ǿ����У������С�ľ��γ�Ϊ��A��B��C�����Ÿ��Ǿ��Σ����磬��ͼ�еľ���A1B1C1D1��A2B2C2D2��AB3C3D3���ǵ�A��B��C�ĸ��Ǿ��Σ����о���AB3C3D3�ǵ�A��B��C�����Ÿ��Ǿ��Σ�

��1����֪A(![]() 2��3)��B(5��0)��C(
2��3)��B(5��0)��C(![]() ��
�� ![]() 2)��
2)��
�ٵ�![]() ʱ����A��B��C�����Ÿ��Ǿ��ε����Ϊ ��
ʱ����A��B��C�����Ÿ��Ǿ��ε����Ϊ ��
������A��B��C�����Ÿ��Ǿ��ε����Ϊ40����t��ֵΪ ��
��2����֪��D(1��1)����E(![]() ��
�� ![]() )�����е�E�Ǻ���
)�����е�E�Ǻ���![]() ��ͼ����һ�㣬��P�ǵ�O��D��E��һ�������С�����Ÿ��Ǿ��ε����Բ�������P�İ뾶r��ȡֵ��Χ��
��ͼ����һ�㣬��P�ǵ�O��D��E��һ�������С�����Ÿ��Ǿ��ε����Բ�������P�İ뾶r��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�
��1�����뾶Ϊ1�ġ�O������A��B��D���ҡ�A��60�㣬���ʱ���εı߳���
��2������PΪAB��һ�㣬������ABCD�ع���P��ֱ��a�۵���ʹ��D����BC���ϣ������̶ȵ�ֱ�ߺ�Բ������ֱ��a����������ͼ�ۼ�������˵�����������ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڶ��κ���y������x��1��2+2��ͼ���У���y��x�������������x��ȡֵ��Χ�ǣ�������
A.x����1B.x��1C.x����1D.x��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ֱ��MN��ֱ��AB��CD�ֱ��ڵ�E��F����1���2������ 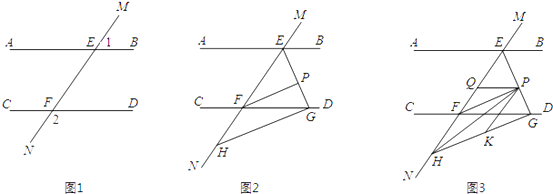
��1�����ж�ֱ��AB��ֱ��CD��λ�ù�ϵ����˵�����ɣ�
��2����ͼ2����BEF���EFD�Ľ�ƽ���߽��ڵ�P��EP��CD���ڵ�G����H��MN��һ�㣬��GH��EG����֤��PF��GH��
��3����ͼ3���ڣ�2���������£�����PH��K��GH��һ��ʹ��PHK=��HPK����PQƽ�֡�EPK���ʡ�HPQ�Ĵ�С�Ƿ����仯�������䣬�������ֵ�����仯��˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com