
【题目】如图,在平行四边形ABCD中,延长BC至E点,使CE=![]() BC,点P是AD边上的动点,以
BC,点P是AD边上的动点,以![]() cm/s的速度从D点到A点方向运动,连接AC、CP、DE.
cm/s的速度从D点到A点方向运动,连接AC、CP、DE.
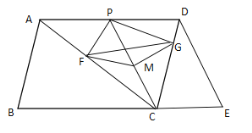
(1)若AD=![]() ,运动时间为t,当四边形PCED为平行四边形时,求t的值;
,运动时间为t,当四边形PCED为平行四边形时,求t的值;
(2)M是CP的中点,PF⊥AC,垂足为F,PG⊥CD,垂足为G,连接MF,MG,求证:∠GMF=2∠ACD.
(3)在(2)的条件下,若∠B=75°,∠ACB=45°,AC=![]() ,连接GF,求△MGF周长的最小值.
,连接GF,求△MGF周长的最小值.
【答案】(1)2s;(2)见解析.(3)(3![]() +6)cm.
+6)cm.
【解析】
(1)根据平行四边形的性质得到PD=CE=![]() AD,即可求出t;
AD,即可求出t;
(2)根据直角三角形斜边上的中线等于斜边的一半得到FC=CM=PM,得到∠PMF=2∠PCF,同理得到∠PMG=2∠PCG,即可证明.
(3)过点M作MN⊥FG于N,有等腰三角形的性质可得MN=![]() MF,NG=FN=
MF,NG=FN=![]() MN=
MN=![]() MF,即可得△MGF周长=
MF,即可得△MGF周长=![]() PC,当PC取最小时,△MGF周长有最小值,有直角三角形的性质可求△MGF周长最小值.
PC,当PC取最小时,△MGF周长有最小值,有直角三角形的性质可求△MGF周长最小值.
(1)∵四边形PCED为平行四边形
∴PD=CE
∵四边形ABCD为平行四边形,∴PD=CE=![]() AD=2
AD=2![]()
故![]() t=2
t=2![]() ,
,
解得t=2s;
(2)∵PF⊥AC,∴△PFC为直角三角形,
∵M是PC的中点,
∴FM=![]() =PM=CM,
=PM=CM,
∴∠MFC=∠MCF,
∴∠PMF=∠MFC+∠MCF =2∠PCF,
∵PG⊥CD,
同理可得∠PMG=2∠PCG,
∴GMF=∠PMF+∠PMG=2∠PCF+2∠PCG=2(∠PCF∠PCG)=2∠ACD,
即∠GMF=2∠ACD.
(3) 如图,过点M作MN⊥FG于N,
∵四边形ABCD是平行四边形
∴∠B=∠ADC=75°,AD//BC
∴∠ADC+∠BCD=180°,∠DAC=∠ACB=45°
∴∠BCD=105°
∴∠ACD=∠BCD-∠ACB=60°
∴∠GMF=120°,且FM=MG
∴∠MGF=∠MFG=30°,且MN⊥FG,FM=MG
∴MN=![]() MF,NG=FN=
MF,NG=FN=![]() MN=
MN=![]() MF
MF
∵△MGF周长=FG+MF+MG=(![]() +2)MF=
+2)MF=![]() PC
PC
∴当PC取最小时,△MGF周长有最小值
∴当PC⊥AD时,PC有最小值
∴此时,∠DAC=45°,PCLAD,AC=6![]() cm,PC=6
cm,PC=6
∴△MGF周长最小值=(3![]() +6)cm
+6)cm


科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=ax2﹣2ax﹣3a(a<0)的图象与x轴交于A、B两点(点A在点B的右侧),与y轴的正半轴交于点C,顶点为D.
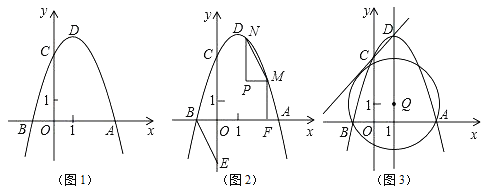
(1)求顶点D的坐标(用含a的代数式表示).
(2)若以AD为直径的圆经过点C.
①求a的值.
②如图2,点E是y轴负半轴上一点,连接BE,将△OBE绕平面内某一点旋转180°,得到△PMN(点P、M、N分别和点O、B、E对应),并且点M、N都在抛物线上,作MF⊥x轴于点F,若线段BF=2MF,求点M、N的坐标.
③如图3,点Q在抛物线的对称轴上,以Q为圆心的圆过A、B两点,并且和直线CD相切,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙商品是按原价打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,某校举办了学生“国学经典大赛”.比赛项目为:![]() .唐诗;
.唐诗;![]() .宋词;
.宋词;![]() .论语;
.论语;![]() .三字经.比赛形式分“单人组”和“双人组”.
.三字经.比赛形式分“单人组”和“双人组”.
(1)小丽参加“单人组”,她从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?
(2)小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则小红和小明都没有抽到“论语”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地出发沿同一路线驶向B地,甲车先出发匀速驶向B地.40分钟后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时,由于满载货物,为了行驶安全,速度减少了50千米/时,结果与甲车同时到达B地.甲乙两车距A地的路 程y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示.请结合图象信息解答下列问题:
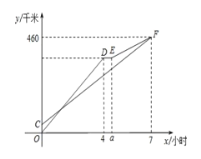
(1)直接写出a的值,并求甲车的速度;
(2)求图中线段EF所表示的y与x的函数关系式,并直接写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=![]() ,OC=
,OC=![]() ,则另一直角边BC的长为__________.
,则另一直角边BC的长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 xOy 中,点 A 是一次函数 y 3x 20 与 y x 12的交点,过点 A 分别作 x 、 y 轴的垂线段,垂足分别是 B 和C ,动点 P 和Q 以1个单位/秒的速度,分别从点C 、 B 出发,沿线段CA 、 BO 方向,向终点 A 、O 运动,设运动时间为t秒.

(1)证明:无论运动时间t 0 t 8取何值,四边形OPAQ 始终为平行四边形;
(2)当四边形OPAQ 为菱形时,请求出此时 PQ 的长度及直线 PQ 的函数解析式;
(3)当OP 满足 2![]() OP 5时,连接 PQ ,直线 PQ 与 y 轴交于点 M ,取线段 AC 的中点 N ,试确定 MNP 的面积 S 与运动的时间t 之间的函数关系式,并求出 S 的取值范围.
OP 5时,连接 PQ ,直线 PQ 与 y 轴交于点 M ,取线段 AC 的中点 N ,试确定 MNP 的面积 S 与运动的时间t 之间的函数关系式,并求出 S 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形ABCO的顶点O在坐标远点,点B的坐标为(1,4),点A在第二象限,反比例函数![]() 的图像经过点A则K的值是()
的图像经过点A则K的值是()
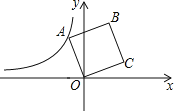
A.-2B.-4C.-8D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一个边长为![]() 的正方形纸片剪去两个小长方形,得到一个“6”的图案,如图2所示,再将剪下的两个小长方形拼成一个新的长方形,如图3所示,
的正方形纸片剪去两个小长方形,得到一个“6”的图案,如图2所示,再将剪下的两个小长方形拼成一个新的长方形,如图3所示,
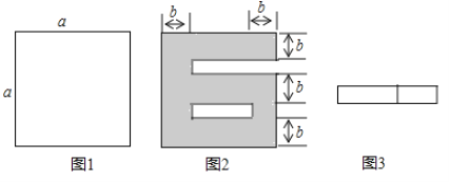
(1)这个新长方形的长和宽分别为________,_________;(用![]() 、
、![]() 的代数式表示)
的代数式表示)
(2)若![]() ,
,![]() ,求这个新长方形的周长.
,求这个新长方形的周长.
(3)在(2)的条件下,当![]() 时,求这个长方形的周长.
时,求这个长方形的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com