
����Ŀ���ס���������A�س�����ͬһ·��ʻ��B�أ��׳��ȳ�������ʻ��B�أ�40���Ӻ��ҳ�������������ʻһ��ʱ�����;�еĻ�վװ����ʱ��Сʱ���������ػ��Ϊ����ʻ��ȫ���ٶȼ�����50ǧ��/ʱ�������׳�ͬʱ����B�أ�����������A�ص�· ��y��ǧ�ף����ҳ���ʻʱ��x��Сʱ��֮��ĺ���ͼ����ͼ��ʾ������ͼ����Ϣ����������⣺
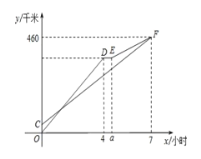
��1��ֱ��д��a��ֵ������׳����ٶȣ�
��2����ͼ���߶�EF����ʾ��y��x�ĺ�����ϵʽ����ֱ��д���Ա���x��ȡֵ��Χ.
���𰸡���1��a=4.5�����ٶ�Ϊ![]() ��ǧ��/Сʱ����2��y=40x+180��4.5��x��7��
��ǧ��/Сʱ����2��y=40x+180��4.5��x��7��
��������
��1����������;��װ����ʱ��Сʱ��֪a=4.5���״�A��B�����ˣ�![]() +7��Сʱ�������ٶȵĹ�ʽ������⣻
+7��Сʱ�������ٶȵĹ�ʽ������⣻
��2������һ��ʼ���ٶ�Ϊvǧ��/Сʱ������������ʱ���ڵ�·�̺��г��������v���ɵ�D��E�����꣬�ٸ��ݴ���ϵ�����������EF�Ľ���ʽ.
��1���������a=4.5��
���ٶ�Ϊ![]() ��ǧ��/Сʱ��
��ǧ��/Сʱ��
��2����һ��ʼ���ٶ�Ϊvǧ��/Сʱ��
��4v+��7-4.5����v-50��=460
���v=90��ǧ��/Сʱ��
��D��4,360����E��4.5��360��
��ֱ��EF�Ľ���ʽΪy=kx+b
��E��4.5��360����F��7,460�������![]() �����
�����![]()
���߶�EF����ʾ��y��x�ĺ�����ϵʽΪy=40x+180��4.5��x��7��


 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д� ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ��ɾ���ֵ�������֪����![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() ��������һ���ԣ����������ǽ⺬�о���ֵ�ķ��̣����磺����
��������һ���ԣ����������ǽ⺬�о���ֵ�ķ��̣����磺����![]() ��
��
��![]() ʱ��ԭ���̿ɻ�Ϊ
ʱ��ԭ���̿ɻ�Ϊ![]() �����
�����![]() ��
��
��![]() ʱ��ԭ���̿ɻ�Ϊ
ʱ��ԭ���̿ɻ�Ϊ![]() �����
�����![]() ��
��
����ԭ���̵Ľ���![]() ��
��![]() ��
��
��1���벹ȫ��Ŀ�к����ϵĽ��ۣ�
��2��������������⣬�ⷽ�̣�![]() ��
��
��3��������![]() �н⣬��
�н⣬��![]() Ӧ����������� ��
Ӧ����������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
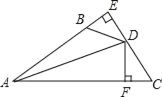
����Ŀ����ͼ��DE��AB��E��DF��AC��F����BD��CD��BE��CF�������н��ۣ���DE��DF����ADƽ�֡�BAC����AE��AD����AC��AB��2BE����ȷ����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
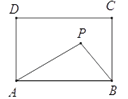
����Ŀ����ͼ���ھ���ABCD�У�AB��5��AD��3������P����![]() �����P��A��B�������֮��PA��PB����СֵΪ�� ��
�����P��A��B�������֮��PA��PB����СֵΪ�� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��y��x+5��x�ύ�ڵ�A��ֱ��y����x+b��x�ύ�ڵ�B��1��0������������ֱ�߽��ڵ�C��
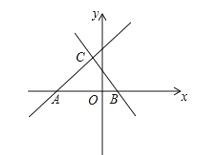
��1����ֱ��BC�Ľ���ʽ�͵�C�����ꣻ
��2��ֱ��д������x�IJ���ʽx+5����x+b�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У��ӳ�BC��E�㣬ʹCE��![]() BC����P��AD���ϵĶ��㣬��
BC����P��AD���ϵĶ��㣬��![]() cm/s���ٶȴ�D�㵽A�㷽���˶�������AC��CP��DE��
cm/s���ٶȴ�D�㵽A�㷽���˶�������AC��CP��DE��
��1����AD=![]() ���˶�ʱ��Ϊt�����ı���PCEDΪƽ���ı���ʱ����t��ֵ��
���˶�ʱ��Ϊt�����ı���PCEDΪƽ���ı���ʱ����t��ֵ��
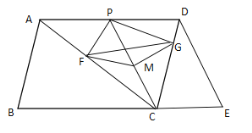
��2��M��CP���е㣬PF��AC������ΪF��PG��CD������ΪG������MF��MG����֤����GMF=2��ACD.
��3���ڣ�2���������£�����B=75������ACB=45����AC=![]() ������GF������MGF�ܳ�����Сֵ.
������GF������MGF�ܳ�����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
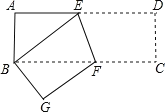
����Ŀ����ͼ���������� ABCD �� EF �۵���ʹ�� D ��� B �غϣ���֪ AB 3 ��AD 9 .
��1���� BE �ij���
��2���� EF �ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һ��С�����壬6�����Ϸֱ���ƽ���ı��Ρ�Բ���������Ρ����Ρ��ȱ������κ�ֱ��������6��ͼ�Σ��������������һ�Σ�����һ���ͼ�μ�����Գ�ͼ�Σ��������ĶԳ�ͼ�εĸ�����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������壩������![]() ��һԪһ�η���
��һԪһ�η���![]() �Ľ�����
�Ľ�����![]() ,��Ƹ÷���Ϊ���Ѻ÷����������磺����
,��Ƹ÷���Ϊ���Ѻ÷����������磺����![]() �Ľ�Ϊ
�Ľ�Ϊ![]() ����
����![]() ����
����![]() Ϊ���Ѻ÷�������
Ϊ���Ѻ÷�������
�������1����![]() ����
����![]() ����
����![]() ���������У�Ϊ���Ѻ÷���������_________����д��ţ���
���������У�Ϊ���Ѻ÷���������_________����д��ţ���
��2��������![]() ��һԪһ�η���
��һԪһ�η���![]() �����Ѻ÷���������
�����Ѻ÷���������![]() ��ֵ��
��ֵ��
��3��������![]() ��һԪһ�η���
��һԪһ�η���![]() �����Ѻ÷������������Ľ�Ϊ
�����Ѻ÷������������Ľ�Ϊ![]() ,��
,��![]() ��
��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com