
【题目】阅读材料:由绝对值的意义可知:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .利用这一特性,可以帮助我们解含有绝对值的方程.比如:方程
.利用这一特性,可以帮助我们解含有绝对值的方程.比如:方程![]() ,
,
当![]() 时,原方程可化为
时,原方程可化为![]() ,解得
,解得![]() ;
;
当![]() 时,原方程可化为
时,原方程可化为![]() ,解得
,解得![]() .
.
所以原方程的解是![]() 或
或![]() .
.
(1)请补全题目中横线上的结论.
(2)仿照上面的例题,解方程:![]() .
.
(3)若方程![]() 有解,则
有解,则![]() 应满足的条件是 .
应满足的条件是 .
科目:初中数学 来源: 题型:
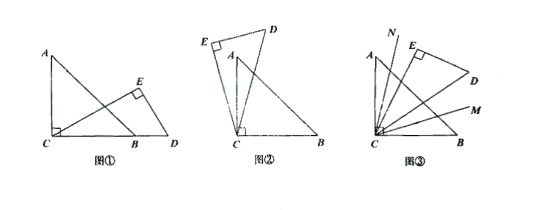
【题目】如图,将一个直角三角板中30°的锐角顶点与另一个直角三角板的直角顶点叠放一起.(注:∠ACB与∠DEC是直角,∠A=45°,∠DEC=30°).
(1)如图①,若点C、B、D在一条直线上,求∠ACE的度数;
(2)如图②,将直角三角板CDE绕点c逆时针方向转动到某个位置,若恰好平分∠DCE,求∠BCD的度数;
(3)如图③若∠DEC始终在∠ACB的内部,分别作射线CM平分∠BCD,射线CN平分∠ACE.如果三角板DCE在∠ACB内绕点C任意转动,∠MCN的度数是否发生变化?如果不变,求出它的度数,如果变化,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名队员参加射击训练,成绩分别绘制成下列两个统计图:
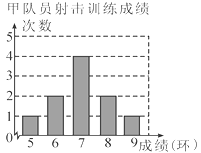
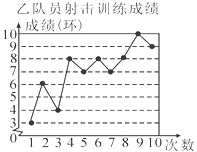
根据以上信息,整理分析数据如下:
平均成绩(环) | 中位数(环) | 众数(环) | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | c |
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击成绩,若选派其中一名参赛,你认为应选哪名队员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以点O为端点按顺时针方向依次作射线OA、OB、OC、OD.
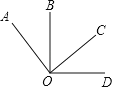
(1)若∠AOC、∠BOD都是直角,∠BOC=60°,求∠AOB和∠DOC的度数.
(2)若∠BOD=100°,∠AOC=110°,且∠AOD=∠BOC+70°,求∠COD的度数.
(3)若∠AOC=∠BOD=α,当α为多少度时,∠AOD和∠BOC互余?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=ax2﹣2ax﹣3a(a<0)的图象与x轴交于A、B两点(点A在点B的右侧),与y轴的正半轴交于点C,顶点为D.
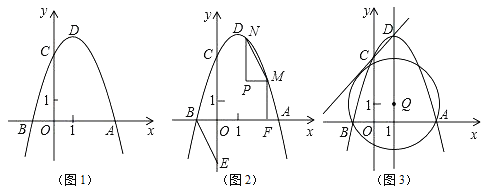
(1)求顶点D的坐标(用含a的代数式表示).
(2)若以AD为直径的圆经过点C.
①求a的值.
②如图2,点E是y轴负半轴上一点,连接BE,将△OBE绕平面内某一点旋转180°,得到△PMN(点P、M、N分别和点O、B、E对应),并且点M、N都在抛物线上,作MF⊥x轴于点F,若线段BF=2MF,求点M、N的坐标.
③如图3,点Q在抛物线的对称轴上,以Q为圆心的圆过A、B两点,并且和直线CD相切,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:数和形是数学的两个主要研究对象,我们经常运用数形结合,树形转化的方法解决一些数学问题,小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1,y1),P2(x2,y2),可通过构造直角三角形利用图1得到结论:P1P2=![]() ,他还利用图2证明了线段P1P2的中点P(x,y),P的坐标公式:x=
,他还利用图2证明了线段P1P2的中点P(x,y),P的坐标公式:x=![]() ,y=
,y=![]() .
.
启发应用:
如图3:在平面直角坐标系中,已知A(8,0),B(0,6),C(1,7),⊙M经过原点O及点A,B,
(1)求⊙M的半径及圆心M的坐标;
(2)判断点C与⊙M的位置关系,并说明理由;
(3)若∠BOA的平分线交AB于点N,交⊙M于点E,分别求出OE的表达式y1,过点M的反比例函数的表达式y2,并根据图象,当y2>y1>0时,请直接写出x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
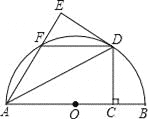
【题目】如图,AB是半圆O的直径,点C为半径OB上一点,过点C作CD丄AB交半圆O于点D,将△ACD沿AD折叠得到△AED,AE交半圆于点F,连接DF.
(1)求证:DE是半圆的切线:
(2)连接0D,当OC=BC时,判断四边形ODFA的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地出发沿同一路线驶向B地,甲车先出发匀速驶向B地.40分钟后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时,由于满载货物,为了行驶安全,速度减少了50千米/时,结果与甲车同时到达B地.甲乙两车距A地的路 程y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示.请结合图象信息解答下列问题:
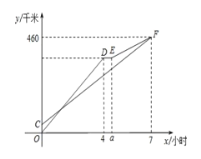
(1)直接写出a的值,并求甲车的速度;
(2)求图中线段EF所表示的y与x的函数关系式,并直接写出自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com