
【题目】如图,以点O为端点按顺时针方向依次作射线OA、OB、OC、OD.
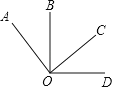
(1)若∠AOC、∠BOD都是直角,∠BOC=60°,求∠AOB和∠DOC的度数.
(2)若∠BOD=100°,∠AOC=110°,且∠AOD=∠BOC+70°,求∠COD的度数.
(3)若∠AOC=∠BOD=α,当α为多少度时,∠AOD和∠BOC互余?并说明理由.
【答案】(1)∠AOB=30°,∠DOC=30°;(2)∠COD=30°;(3)当α=45°时,∠AOD与∠BOC互余.
【解析】
(1)根据互余的意义,即可求出答案;
(2)设出未知数,利用题目条件,表示出∠AOB、∠BOC,进而列方程求解即可;
(3)利用角度的和与差,反推得出结论,再利用互余得出答案.
(1)∵∠AOC=90°,∠BOD=90°,∠BOC=60°,
∴∠AOB=∠AOC﹣∠BOC=90°﹣60°=30°,
∠DOC=∠BOD﹣∠BOC=90°﹣60°=30°;
(2)设∠COD=x°,则∠BOC=100°﹣x°.
∵∠AOC=110°,
∴∠AOB=110°﹣(100°﹣x°)=x°+10°.
∵∠AOD=∠BOC+70°,
∴100°+10°+x°=100°﹣x°+70°,
解得:x=30,
即∠COD=30°;
(3)当α=45°时,∠AOD与∠BOC互余.理由如下:
要使∠AOD与∠BOC互余,即∠AOD+∠BOC=90°,
∴∠AOB+∠BOC+∠COD+∠BOC=90°,
即∠AOC+∠BOD=90°.
∵∠AOC=∠BOD=α,
∴∠AOC=∠BOD=45°,
即α=45°,
∴当α=45°时,∠AOD与∠BOC互余.



科目:初中数学 来源: 题型:
【题目】已知:点![]() 在同一条直线上,点
在同一条直线上,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 的中点.
的中点.
(1)如图1 ,当点![]() 在线段
在线段![]() 上时.
上时.
①若![]() ,则线段
,则线段![]() 的长为_______.
的长为_______.
②若点![]() 为线段
为线段![]() 上任意一点,
上任意一点, ![]() ,则线段
,则线段![]() 的长为_______. ( 用含
的长为_______. ( 用含![]() 的代数式表示)
的代数式表示)
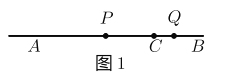
(2)如图2 ,当点![]() 不在线段
不在线段![]() 上时,若
上时,若![]() ,求
,求![]() 的长(用含
的长(用含![]() 的代数式表示) .
的代数式表示) .
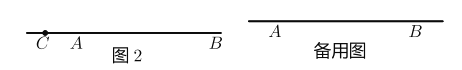
(3)如图,已知![]() ,作射线
,作射线![]() ,若射线
,若射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() .
.
①当射线![]() 在
在![]() 的内部时,则
的内部时,则![]() =________°.
=________°.
②当射线![]() 在
在 ![]() 的外部时,则
的外部时,则![]() =_______°. ( 用含
=_______°. ( 用含![]() 的代数式表示) .
的代数式表示) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MAN=120°,AC平分∠MAN.B、D分别在射线AN、AM上.
(1)在图1中,当∠ABC=∠ADC=90°时,求证:AD+AB=AC
(2)若把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°,其他条件不变,如图2所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.

(图1) (图2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1:y=-2x+4与x、y轴分别交于点N、C,与直线l2:y=kx+b(k≠0)交于点M,点M的横坐标为1,直线l2与x轴的交点为A(-2,0)
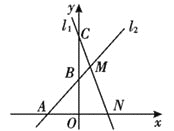
(1)求k,b的值;
(2)求四边形MNOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AB上一点,点D为BC的中点,且AB=18cm,AC=4CD.
(1)图中共有 条线段;
(2)求AC的长;
(3)若点E在直线AB上,且EA=2cm,求BE的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC且AB=BC,DE⊥CD且DE=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是( )
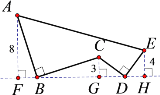
A. 36B. 48C. 72D. 108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:由绝对值的意义可知:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .利用这一特性,可以帮助我们解含有绝对值的方程.比如:方程
.利用这一特性,可以帮助我们解含有绝对值的方程.比如:方程![]() ,
,
当![]() 时,原方程可化为
时,原方程可化为![]() ,解得
,解得![]() ;
;
当![]() 时,原方程可化为
时,原方程可化为![]() ,解得
,解得![]() .
.
所以原方程的解是![]() 或
或![]() .
.
(1)请补全题目中横线上的结论.
(2)仿照上面的例题,解方程:![]() .
.
(3)若方程![]() 有解,则
有解,则![]() 应满足的条件是 .
应满足的条件是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AB=6, ∠BAC=30, ∠BAC的平分线交BC于点D,E,F分别是线段AD和AB上的动点,则BE+EF的最小值是___
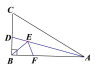
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com