
【题目】如图,AB⊥BC且AB=BC,DE⊥CD且DE=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是( )
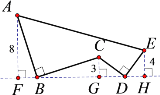
A. 36B. 48C. 72D. 108
科目:初中数学 来源: 题型:
【题目】如图 .在数轴.上有![]() 两个点(点
两个点(点![]() 在点
在点![]() 的左侧) ,
的左侧) , ![]()
![]()
(1)如果点![]() 表示的数是
表示的数是![]() ,那么,
,那么,
①点![]() 表示的数是_______.
表示的数是_______.
②如果点![]() 从点
从点![]() 出发,沿数轴正方向运动,速度是每秒3个单位长度,运动秒后,点
出发,沿数轴正方向运动,速度是每秒3个单位长度,运动秒后,点![]() 表示的数是_______.( 用含
表示的数是_______.( 用含![]() 的代数式表示) ; 经过________秒 ,
的代数式表示) ; 经过________秒 , ![]() .
.
(2)如果点![]() 表示的数是
表示的数是![]() ,将数轴的负半轴绕原点
,将数轴的负半轴绕原点![]() 顺时针旋转60° ,得到
顺时针旋转60° ,得到![]() ,如图2所示,射线
,如图2所示,射线![]() 从
从![]() 出发绕点
出发绕点![]() 顺时针旋转,速度是每秒15° ,同时,射线
顺时针旋转,速度是每秒15° ,同时,射线![]() 从
从![]() 出发绕点
出发绕点![]() 逆时针旋转,速度是每秒5° .设运动时间为
逆时针旋转,速度是每秒5° .设运动时间为![]() 秒,当
秒,当![]() 秒时,
秒时, ![]() 停止运动.
停止运动.
①当![]() 为________秒时,
为________秒时,![]() 与
与![]() 重合.
重合.
②当![]() 时,
时,![]() 的值是________.
的值是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,按下列方法将数轴的正半轴绕在一个圆上(该圆周长为![]() 个单位长,且在圆周的三等分点处分别标上了数字
个单位长,且在圆周的三等分点处分别标上了数字![]() ,
,![]() ,
,![]() )上:先让原点与圆周上
)上:先让原点与圆周上![]() 所对应的点重合,再将正半轴按顺时针方向绕在该圆周上,使数轴上
所对应的点重合,再将正半轴按顺时针方向绕在该圆周上,使数轴上![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 所对应的点分别与圆周上
所对应的点分别与圆周上![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 所对应的点重合,这样,正半轴上的整数就与圆周上的数字建立了一种对应关系.
所对应的点重合,这样,正半轴上的整数就与圆周上的数字建立了一种对应关系.
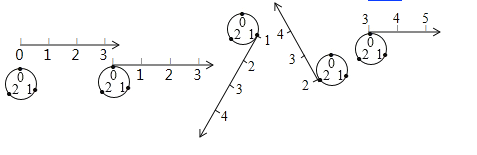
(1)圆周上数字![]() 与数轴上的数
与数轴上的数![]() 对应,则
对应,则![]() __________.
__________.
(2)数轴上的一个整数点刚刚绕过圆周![]() 圈(
圈(![]() 为正整数)后,并落在圆周上数字
为正整数)后,并落在圆周上数字![]() 所对应的位置,这个整数是____________.(用含
所对应的位置,这个整数是____________.(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某化工车间发生有害气体泄漏,自泄漏开始到完全控制利用了40min,之后将对泄漏有害气体进行清理,线段DE表示气体泄漏时车间内危险检测表显示数据y与时间x(min)之间的函数关系(0≤x≤40),反比例函数y=![]() 对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:
对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:
(1)危险检测表在气体泄漏之初显示的数据是 ;
(2)求反比例函数y=![]() 的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.
的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以点O为端点按顺时针方向依次作射线OA、OB、OC、OD.
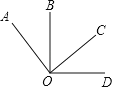
(1)若∠AOC、∠BOD都是直角,∠BOC=60°,求∠AOB和∠DOC的度数.
(2)若∠BOD=100°,∠AOC=110°,且∠AOD=∠BOC+70°,求∠COD的度数.
(3)若∠AOC=∠BOD=α,当α为多少度时,∠AOD和∠BOC互余?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:某商场第一季度销售甲、乙两种冰箱若干台,其中乙种冰箱的数量比甲种冰箱多销售![]() 台,第二季度甲种冰箱的销量比第一季度增加
台,第二季度甲种冰箱的销量比第一季度增加![]() ,乙种冰箱的销量比第一季度增加
,乙种冰箱的销量比第一季度增加![]() ,且两种冰箱的总销量达到
,且两种冰箱的总销量达到![]() 台.
台.
求:(1)该商场第一季度销售甲种冰箱多少台?
(2)若每台甲种冰箱的利润为![]() 元,每台乙种冰箱的利润为
元,每台乙种冰箱的利润为![]() 元,则该商场第二季度销售冰箱的总利润是多少元?
元,则该商场第二季度销售冰箱的总利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=ax2﹣2ax﹣3a(a<0)的图象与x轴交于A、B两点(点A在点B的右侧),与y轴的正半轴交于点C,顶点为D.
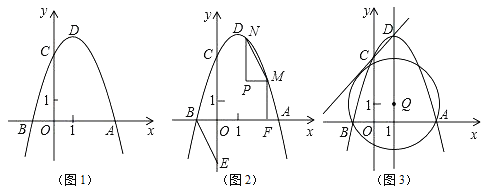
(1)求顶点D的坐标(用含a的代数式表示).
(2)若以AD为直径的圆经过点C.
①求a的值.
②如图2,点E是y轴负半轴上一点,连接BE,将△OBE绕平面内某一点旋转180°,得到△PMN(点P、M、N分别和点O、B、E对应),并且点M、N都在抛物线上,作MF⊥x轴于点F,若线段BF=2MF,求点M、N的坐标.
③如图3,点Q在抛物线的对称轴上,以Q为圆心的圆过A、B两点,并且和直线CD相切,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面文字后,解答问题
有这样一道题目:“已知:二次函数![]() 的图象经过点(1,0)_________,
的图象经过点(1,0)_________,
求证:这个二次函数图象关于直线![]() 对称”
对称”
题目中的横线部分是一段被墨水污染了无法辨认的文字.
根据现有信息,题目中二次函数图象不具有的性质是( )
A. 过点(3,0) B. 顶点是(2,-2)
C. 在X轴上截得的线段长是2 D. 与Y轴交点是(0,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,某校举办了学生“国学经典大赛”.比赛项目为:![]() .唐诗;
.唐诗;![]() .宋词;
.宋词;![]() .论语;
.论语;![]() .三字经.比赛形式分“单人组”和“双人组”.
.三字经.比赛形式分“单人组”和“双人组”.
(1)小丽参加“单人组”,她从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?
(2)小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则小红和小明都没有抽到“论语”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com