
����Ŀ����֪����![]() ��ͬһ��ֱ���ϣ���
��ͬһ��ֱ���ϣ���![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬��
���е㣬��![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣮
���е㣮
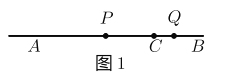
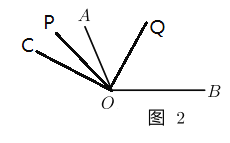
��1����ͼ1 ������![]() ���߶�
���߶�![]() ��ʱ��
��ʱ��
����![]() �����߶�
�����߶�![]() �ij�Ϊ_______��
�ij�Ϊ_______��
������![]() Ϊ�߶�
Ϊ�߶�![]() ������һ�㣬
������һ�㣬 ![]() �����߶�
�����߶�![]() �ij�Ϊ_______�� �� �ú�
�ij�Ϊ_______�� �� �ú�![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
��2����ͼ2 ������![]() �����߶�
�����߶�![]() ��ʱ����
��ʱ����![]() ����
����![]() �ij����ú�
�ij����ú�![]() �Ĵ���ʽ��ʾ�� ��
�Ĵ���ʽ��ʾ�� ��
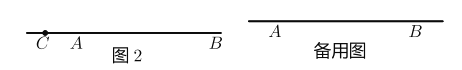
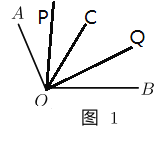
��3����ͼ����֪![]() ��������
��������![]() ��������
��������![]() ƽ��
ƽ��![]() ������
������![]() ƽ��
ƽ��![]() ��
��
�ٵ�����![]() ��
��![]() ���ڲ�ʱ����
���ڲ�ʱ����![]() =________�㣮
=________�㣮
�ڵ�����![]() ��
�� ![]() ���ⲿʱ����
���ⲿʱ����![]() =_______���� �� �ú�
=_______���� �� �ú�![]() �Ĵ���ʽ��ʾ�� ��
�Ĵ���ʽ��ʾ�� ��
���𰸡���1����5����![]() ����2��
����2�� ![]() ����3����
����3����![]() ����
����![]() ��
��
��������
(1) �������PC=4,QC=1�������߶�![]() �ij����ɣ�
�ij����ɣ�
�������PC= ![]() AC,QC=
AC,QC=![]() BC��������m��ʾ�߶�
BC��������m��ʾ�߶�![]() �ij���
�ij���
(2) ����![]() �����߶�
�����߶�![]() ��ʱ�������PC=
��ʱ�������PC= ![]() AC,QC=
AC,QC=![]() BC������ͼ����m��ʾ�߶�
BC������ͼ����m��ʾ�߶�![]() �ij����ɣ�
�ij����ɣ�
(3))���Ȱ������⻭��ͼ�Σ���OC�ڡ�AOB�ڲ����ⲿ����������������POC= ![]() ��AOC,��COQ=
��AOC,��COQ=![]() ��COB���ٸ���ͼ���ñ�ʾ
��COB���ٸ���ͼ���ñ�ʾ![]() ���ɣ�
���ɣ�
�⣺(1) �١�![]() ����
����![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬��
���е㣬��![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬
���е㣬
��PC=4,QC=1��
��PQ=PC+QC=5��
�ʴ�Ϊ5��
�ڵ�![]() Ϊ�߶�
Ϊ�߶�![]() ������һ�㣬
������һ�㣬 ![]() ����
����![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬��
���е㣬��![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬
���е㣬
��PC= ![]() AC,QC=
AC,QC=![]() BC��
BC��
��PQ=PC+QC=![]() AC+
AC+![]() BC=
BC=![]() AB=
AB=![]() m��
m��
�ʴ�Ϊ![]() m.
m.
(2)����C���߶�BA���ӳ���ʱ����ͼ2��
![]() ����
����![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬��
���е㣬��![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬
���е㣬
��PC= ![]() AC,QC=
AC,QC= ![]() BC��
BC��
��PQ=QC-PC=![]() BC-
BC-![]() AC=
AC=![]() AB=
AB=![]() m��
m��
����C���߶�AB���ӳ���ʱ����ͼ3��
![]() ����
����![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬��
���е㣬��![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬
���е㣬
��PC= ![]() AC,QC=
AC,QC= ![]() BC��
BC��
��PQ=PC-QC=![]() AC-
AC-![]() BC=
BC=![]() AB=
AB=![]() m��
m��
�൱��![]() �����߶�
�����߶�![]() ��ʱ����
��ʱ����![]() ��
�� ![]() �ij�Ϊ
�ij�Ϊ![]() m.
m.
(3) �ٵ�����![]() ��
��![]() ���ڲ�ʱ����ͼ1��
���ڲ�ʱ����ͼ1��
������![]() ƽ��
ƽ��![]() ������
������![]() ƽ��
ƽ��![]()
���POC= ![]() ��AOC,��COQ=
��AOC,��COQ=![]() ��COB��
��COB��
���POQ=��POC+��COQ= ![]() ��AOC+
��AOC+![]() ��COB =
��COB =![]() ��AOB=
��AOB=![]() ,
,
�ʴ�Ϊ![]() ;
;
�ڵ�����![]() ��
�� ![]() ���ⲿʱ����ͼ2
���ⲿʱ����ͼ2
������![]() ƽ��
ƽ��![]() ������
������![]() ƽ��
ƽ��![]()
���POC= ![]() ��AOC,��COQ=
��AOC,��COQ=![]() ��COB��
��COB��
���POQ=��QOC-��COP= ![]() ��COB-
��COB-![]() ��AOC =
��AOC =![]() ��AOB=
��AOB=![]() ;
;
�ʴ�Ϊ![]() .
.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�ı�OA��x���ϣ���ƽ���ı����ضԽ���AC���ۣ�AO�Ķ�Ӧ�߶�ΪAD���ҵ�D��C��O��ͬһ��ֱ���ϣ�AD��BC���ڵ�E.
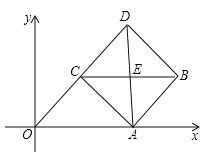
��1����֤����ABC�ա�CDA.
��2����ֱ��AB�ĺ�������ʽΪ![]() ����������ACE�����.
����������ACE�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����оٰ���������ۣ�������������У��ס��������ڱ���ʱ��·��![]() ���ף���ʱ��
���ף���ʱ��![]() �����ӣ�֮��ĺ�����ϵͼ����ͼ��ʾ������ͼ��õ����н��ۣ�����Ϊ��ȷ�Ľ����ǣ� ��
�����ӣ�֮��ĺ�����ϵͼ����ͼ��ʾ������ͼ��õ����н��ۣ�����Ϊ��ȷ�Ľ����ǣ� ��
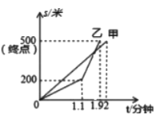
����α�����ȫ����![]() �ף����Ҷ��ȵ����յ㣻�۱��������Ӵӳ�����
�ף����Ҷ��ȵ����յ㣻�۱��������Ӵӳ�����![]() ����ʱ��Σ��Ҷӵ��ٶȱȼӵ��ٶȿ죻�����������ʱ�ҵ��ٶ���
����ʱ��Σ��Ҷӵ��ٶȱȼӵ��ٶȿ죻�����������ʱ�ҵ��ٶ���![]() ��/���ӣ�����
��/���ӣ�����![]() ����ʱ���Ҷ����˼�.
����ʱ���Ҷ����˼�.
A.�٢ۢ�B.�٢ڢ�C.�٢ڢ�D.�٢ڢۢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�ų�Ϊ8cm����Ϊ6cm�ľ���ֽƬ�ϣ���Ҫ����һ������Ϊ5cm�ĵ��������Σ�Ҫ���������ε�һ����������ε�һ�������غϣ���������������ھ��εı��ϣ�������µĵ��������ε����Ϊ______cm2��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
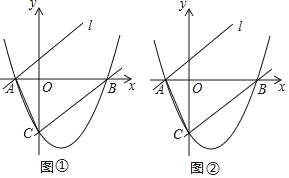
����Ŀ����ͼ��ʾ��������y=![]() ��
��![]() x��4��x�ύ�ڵ�A��B����y ���ཻ�ڵ�C��
x��4��x�ύ�ڵ�A��B����y ���ཻ�ڵ�C��
��1����ֱ��BC�Ľ���ʽ��
��2����ֱ��BC����ƽ�ƺ���A�õ�ֱ��l��y=mx+n����D��ֱ��l�ϣ�����A��B��C��DΪ������ı�����ƽ���ı��Σ������D�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ �������ᣮ����![]() �����㣨��
�����㣨��![]() �ڵ�
�ڵ�![]() ����ࣩ ��
����ࣩ �� ![]()
![]()
��1�������![]() ��ʾ������
��ʾ������![]() ����ô��
����ô��
�ٵ�![]() ��ʾ������_______��
��ʾ������_______��
�������![]() �ӵ�
�ӵ�![]() �������������������˶����ٶ���ÿ��3����λ���ȣ��˶����
�������������������˶����ٶ���ÿ��3����λ���ȣ��˶����![]() ��ʾ������_______���� �ú�
��ʾ������_______���� �ú�![]() �Ĵ���ʽ��ʾ�� �� ����________�� ��
�Ĵ���ʽ��ʾ�� �� ����________�� �� ![]() ��
��
��2�������![]() ��ʾ������
��ʾ������![]() ��������ĸ�������ԭ��
��������ĸ�������ԭ��![]() ˳ʱ����ת60�� ���õ�
˳ʱ����ת60�� ���õ�![]() ����ͼ2��ʾ������
����ͼ2��ʾ������![]() ��
��![]() �����Ƶ�
�����Ƶ�![]() ˳ʱ����ת���ٶ���ÿ��15�� ��ͬʱ������
˳ʱ����ת���ٶ���ÿ��15�� ��ͬʱ������![]() ��
��![]() �����Ƶ�
�����Ƶ�![]() ��ʱ����ת���ٶ���ÿ��5�� �����˶�ʱ��Ϊ
��ʱ����ת���ٶ���ÿ��5�� �����˶�ʱ��Ϊ![]() �룬��
�룬��![]() ��ʱ��
��ʱ�� ![]() ֹͣ�˶���
ֹͣ�˶���
�ٵ�![]() Ϊ________��ʱ��
Ϊ________��ʱ��![]() ��
��![]() �غϣ�
�غϣ�
�ڵ�![]() ʱ��
ʱ��![]() ��ֵ��________��
��ֵ��________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ��ֱ�����ǰ���30������Ƕ�������һ��ֱ�����ǰ��ֱ�Ƕ������һ��.��ע����ACB����DEC��ֱ�ǣ���A=45�㣬��DEC=30�㣩.
��1����ͼ�٣�����C��B��D��һ��ֱ���ϣ�����ACE�Ķ�����
��2����ͼ�ڣ���ֱ�����ǰ�CDE�Ƶ�c��ʱ�뷽��ת����ij��λ�ã���ǡ��ƽ����DCE������BCD�Ķ�����
��3����ͼ������DECʼ������ACB���ڲ����ֱ�������CMƽ����BCD,����CNƽ����ACE.������ǰ�DCE����ACB���Ƶ�C����ת������MCN�Ķ����Ƿ����仯��������䣬������Ķ���������仯��˵��������
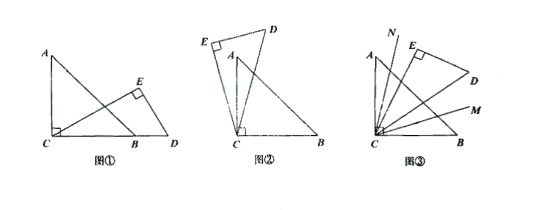
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��֯ѧ�������80km�Ľ�����ɽ�����������ʵ���������8��00ѧ���˳�;������ѧУ����������8��30һλ��ʦ���������ٵ���ѧ����С�γ���ѧУ���������С�γ��ȳ�;������10���ӵ���Ŀ�ĵأ�
��1��С��������ʻʱ��ȳ�;��������ʻʱ���� Сʱ������ֱ��д���𰸣�
��2����֪С�γ���ƽ���ٶ��dz�;������1.5������С�γ����ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Ե�OΪ�˵㰴˳ʱ�뷽������������OA��OB��OC��OD.
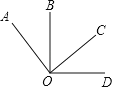
��1������AOC����BOD����ֱ�ǣ���BOC��60�������AOB�͡�DOC�Ķ���.
��2������BOD��100������AOC��110�����ҡ�AOD����BOC+70�������COD�Ķ���.
��3������AOC����BOD����������Ϊ���ٶ�ʱ����AOD�͡�BOC���ࣿ��˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com