
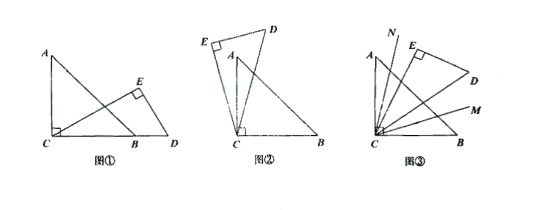
����Ŀ����ͼ����һ��ֱ�����ǰ���30������Ƕ�������һ��ֱ�����ǰ��ֱ�Ƕ������һ��.��ע����ACB����DEC��ֱ�ǣ���A=45�㣬��DEC=30�㣩.
��1����ͼ�٣�����C��B��D��һ��ֱ���ϣ�����ACE�Ķ�����
��2����ͼ�ڣ���ֱ�����ǰ�CDE�Ƶ�c��ʱ�뷽��ת����ij��λ�ã���ǡ��ƽ����DCE������BCD�Ķ�����
��3����ͼ������DECʼ������ACB���ڲ����ֱ�������CMƽ����BCD,����CNƽ����ACE.������ǰ�DCE����ACB���Ƶ�C����ת������MCN�Ķ����Ƿ����仯��������䣬������Ķ���������仯��˵��������
���𰸡���1��60������2��75������3�����䣬60��
��������
��1�����á�ACE=��BCA-��DCE���м��㣻
��2������CAǡ��ƽ�֡�DCE�õ���DCA=![]() ��DCE=15����Ȼ����ݡ�BCD=��BCA-��DCA���м��㣻
��DCE=15����Ȼ����ݡ�BCD=��BCA-��DCA���м��㣻
��3���ȸ���CMƽ�֡�BCD��CNƽ�֡�ACE�õ���ECN=![]() ��ACE����DCM=
��ACE����DCM=![]() ��BCD�����ECN+��DCM=
��BCD�����ECN+��DCM=![]() ����BCA-��DCE�������ԡ�MCN=��ECN+��DCM+��DCE=
����BCA-��DCE�������ԡ�MCN=��ECN+��DCM+��DCE=![]() ����BCA+��DCE����Ȼ��ѡ�BCA=90�㣬��DCE=30��������㼴�ɣ�
����BCA+��DCE����Ȼ��ѡ�BCA=90�㣬��DCE=30��������㼴�ɣ�
�⣺��1���ߡ�BCA=90�㣬��DCE=30�㣬
���ACE=��BCA-��DCE=60�㣻
��2����CAǡ��ƽ�֡�DCE��
���DCA=![]() ��DCE=
��DCE=![]() ��30��=15�㣬
��30��=15�㣬
���BCD=��BCA-��DCA=90��-15��=75�㣻
��3����MCN�Ķ����������仯����MCN=60�����������£�
��CMƽ�֡�BCD��CNƽ�֡�ACE��
���ECN=![]() ��ACE����DCM=
��ACE����DCM=![]() ��BCD��
��BCD��
���ECN+��DCM=![]() ����ACE+��BCD��=
����ACE+��BCD��=![]() ����BCA-��DCE����
����BCA-��DCE����
���MCN=��ECN+��DCM+��DCE
=![]() ����BCA+��DCE��=
����BCA+��DCE��=![]() ����90��+30�㣩=60�㣮
����90��+30�㣩=60�㣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
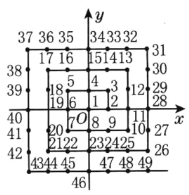
����Ŀ��������������ͼ��ʾ�Ĺ�����ƽ��ֱ������ϵ�н�������,ÿ����������Ӧһ����������(x,y),��x,y��Ϊ����,����5��Ӧ������Ϊ(-1,1),��̽��2015��Ӧ������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)��ͼ��ƽ��������ABC��ʹ��Aƽ�Ƶ���![]() ������ƽ�ƺ��������
������ƽ�ƺ��������![]() ;
;
(2)��(1)�������£�ָ����A,B,C �Ķ�Ӧ�㣬��ָ��AB,BC,AC�Ķ�Ӧ�߶κ͡�A����B, ��C�Ķ�Ӧ��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=ax2+bx+c��a��0����ͼ��A����1��0����B��4��0����C��0��2�����㣮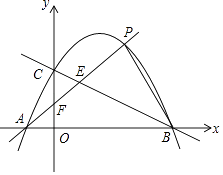
��1����ö��κ����Ľ���ʽ��
��2����D�Ǹö��κ���ͼ���ϵ�һ�㣬�������DBA=��CAO��O������ԭ�㣩�����D�����ꣻ
��3����P�Ǹö��κ���ͼ����λ��һ�����ϵ�һ���㣬����PA�ֱ�BC��y�����E��F������PEB����CEF������ֱ�ΪS1��S2 �� ��S1��S2�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Сǿ��Уѧ���������������������˽�����ͬѧ�Ǹ�ϲ��ʲô�����˶����Ա�ѧ������֯�ܻ�ӭ�ı���.����������˵����ʾ�����ȫУÿ������ѡȡ��һ��������ѧ�����е��飬�����ʾ�������
�����ʾ�
����ϲ���������˶����� ������ѡ��
A������B������C������D��ƹ����E����ë��F������
�����ʾ�
����ϲ���������˶����� ������ѡ��
A������B������C������D��ƹ����E����ë��F������
Сǿ����ͳ�����������ĸ��С�������ֲ������ͳ�Ʊ�������ͳ��ͼ����
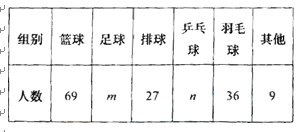

��1������д��ͳ�Ʊ��п�ȱ���ֵ�����m= , n= .
��2��������ͳ��ͼ�У���ë������Ӧ������Բ�Ľǵ��� .
��3��������ݵ���������Сǿ������Ҫ��������������Ľ��飮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABCD�У��Խ���AC��BD�ཻ�ڵ�O����AB=4��BD=10��sin��BDC= ![]() ����ABCD������� ��
����ABCD������� �� 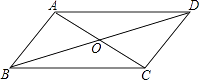
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ��Լˮ��Դ���ƶ����µľ�����ˮ�շѱ��������±����û�ÿ�½��ɵ�ˮ��y��Ԫ����ÿ����ˮ��x��m3��֮��Ĺ�ϵ��ͼ��ʾ�� 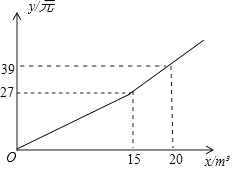
��1����y����x�ĺ�������ʽ��
��2����ij�û��������·ݹ���ˮ40cm3�����·���ˮ��������25cm3��������ˮ��79.8Ԫ������û��������·ݵ���ˮ�����Ƕ���m3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=kx+b��k��0����˫����y= ![]() ��m��0���ཻ��A��1��2����B��n����1�����㣮
��m��0���ཻ��A��1��2����B��n����1�����㣮 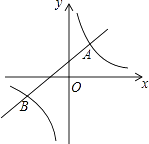
��1����˫���ߵĽ���ʽ��
��2����A1��x1 �� y1����A2��x2 �� y2����A3��x3 �� y3��Ϊ˫�����ϵ����㣬��x1��0��x2��x3 �� ��ֱ��д��y1 �� y2 �� y3�Ĵ�С��ϵ��
��3���۲�ͼ����ֱ��д������ʽkx+b�� ![]() �Ľ⼯��
�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ѧ�������Ķ���ϲ�ã�ijУ�Ӱ��꼶�����ȡ����ѧ�������ʾ����飬����Ҫ��ÿ��ֻѡȡһ��ϲ�����鼮�����û��ϲ�����鼮����������������ͳ�ơ�ͼ��1����ͼ��2�����������ݺ���Ƶ�������������ͳ��ͼ�����½��۲���ȷ���ǣ� ��
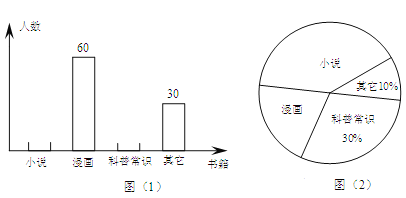
A. ��������ͳ��ͼ��֪ϲ�������ճ�ʶ����ѧ����90�ˣ�
B. �����꼶����1200��ѧ��������������ͳ��ͼ�ɹ���ϲ�������ճ�ʶ����ѧ��Լ��360����
C. ��������ͳ��ͼ����ȷ��ϲ����С˵����������
D. ������ͳ��ͼ�У����������������ε�Բ�Ľ�Ϊ72����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com