
【题目】在ABCD中,对角线AC,BD相交于点O,若AB=4,BD=10,sin∠BDC= ![]() ,则ABCD的面积是 .
,则ABCD的面积是 . 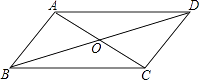
【答案】24
【解析】解:作OE⊥CD于E,如图所示: ∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD= ![]() BD=5,CD=AB=4,
BD=5,CD=AB=4,
∵sin∠BDC= ![]() =
= ![]() ,
,
∴OE=3,
∴DE= ![]() =4,
=4,
∵CD=4,
∴点E与点C重合,
∴AC⊥CD,OC=3,
∴AC=2OC=6,
∴ABCD的面积=CDAC=4×6=24;
所以答案是:24.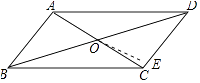
【考点精析】关于本题考查的平行四边形的性质和解直角三角形,需要了解平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】2016年9月10日,郑徐高铁正式运营.从徐州到郑州全程约360km,高铁开通后,运行时间比特快列车所用的时间减少了2.1小时.若高铁列车的平均速度是特快列车平均速度的2.4倍,求特快列车的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,隧道的截面由半圆和长方形构成,长方形的长BC为8m,宽AB为1m,该隧道内设双向行驶的车道(共有2条车道),若现有一辆货运卡车高4m,宽2.3m。则这辆货运卡车能否通过该隧道?说明理由.
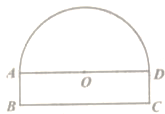
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,已知点C在线段AB上,且AC=5cm,BC=3cm,点M,N分别是AC,BC的中点,求线段MN的长度.
(2)若点C是线段AB上任意一点,且AC=a,BC=b, 点M、N分别是,AC,BC的中点,请直接写出线段MN的长度(用含a,b的代数式表示)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个直角三角板中30°的锐角顶点与另一个直角三角板的直角顶点叠放一起.(注:∠ACB与∠DEC是直角,∠A=45°,∠DEC=30°).
(1)如图①,若点C、B、D在一条直线上,求∠ACE的度数;
(2)如图②,将直角三角板CDE绕点c逆时针方向转动到某个位置,若恰好平分∠DCE,求∠BCD的度数;
(3)如图③若∠DEC始终在∠ACB的内部,分别作射线CM平分∠BCD,射线CN平分∠ACE.如果三角板DCE在∠ACB内绕点C任意转动,∠MCN的度数是否发生变化?如果不变,求出它的度数,如果变化,说明理由。
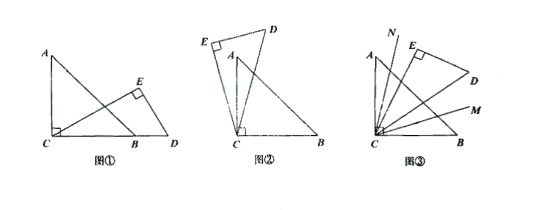
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E, 
(1)求证:DE=DB;
(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DBE中,BC=BE,还需要添加两个条件才能使△ABC≌△DBE,则不能添加的一组条件是( )
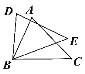
A. AC=DE,∠C=∠E B. BD=AB,AC=DE C. AB=DB,∠A=∠D D. ∠C=∠E,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将含45°角的三角板的直角顶点R放在直线l上,分别过两锐角的顶点M,N作l的垂线,垂足分别为P、Q,
(1)如图1,观察图1可知:与NQ相等的线段是 , 与∠NPQ相等的角是 . 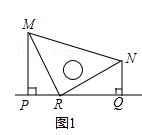
(2)直角△ABC中,∠B=90°,在AB边上任取一点D,连接CD,分别以AC,DC为边作正方形ACEF和正方形CDGH,如图2,过E,H分别作BC所在直线的垂线,垂足分别为K,L.试探究EK与HL之间的数量关系,并证明你的结论.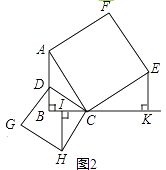
(3)直角△ABC中,∠B=90°,在AB边上任取一点D,连接CD,分别以AC,DC为边作矩形ACEF和矩形CDGH,连接EH交BC所在的直线于点T,如图3,如果AC=kCE,CD=kCH,试探究TE与TH之间的数量关系,并证明你的结论.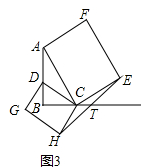
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列各题:
(1)如图,已知直线AB与⊙O相切于点C,且AC=BC,求证:OA=OB. 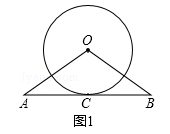
(2)如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AB=3,求AC的长. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com