
����Ŀ������45��ǵ����ǰ��ֱ�Ƕ���R����ֱ��l�ϣ��ֱ������ǵĶ���M��N��l�Ĵ��ߣ�����ֱ�ΪP��Q��
��1����ͼ1���۲�ͼ1��֪����NQ��ȵ��߶��� �� ���NPQ��ȵĽ��� �� 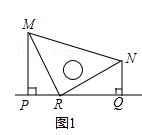
��2��ֱ�ǡ�ABC�У���B=90�㣬��AB������ȡһ��D������CD���ֱ���AC��DCΪ����������ACEF��������CDGH����ͼ2����E��H�ֱ���BC����ֱ�ߵĴ��ߣ�����ֱ�ΪK��L����̽��EK��HL֮���������ϵ����֤����Ľ��ۣ�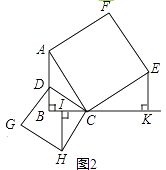
��3��ֱ�ǡ�ABC�У���B=90�㣬��AB������ȡһ��D������CD���ֱ���AC��DCΪ��������ACEF�;���CDGH������EH��BC���ڵ�ֱ���ڵ�T����ͼ3�����AC=kCE��CD=kCH����̽��TE��TH֮���������ϵ����֤����Ľ��ۣ�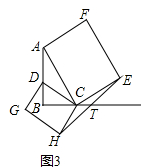
���𰸡�
��1��PR����PMR
��2��
�⣺���ı���ACEF�������Σ�
��AC=CE����ACE=90�㣬
��EK��BK��
���B=��EKC=90�㣬
���BAC+��ACB=��ACB+��ECK=90�㣬
���BAC=��ECK��
�ڡ�ABC���CEK�У�  ��
��
���ABC�ա�CEK��
��EK=BC��
���ı���CDGH�������Σ���CD=CH����DCH=90�㣬
��HI��BC��
���B=��CIH=90�㣬
���DCB+��ICK=��ICK+��CHI=90�㣬���DCB=��CHI��
�ڡ�DCB���CHI�У� 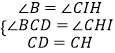 �����DCB�ա�CHI��
�����DCB�ա�CHI��
��BC=HI��
��EK=IH
��3��
�⣺��ͼ3����E��EM��BC��M����H��HN��BC��N��
���ı���ACEF�Ǿ��Σ�
���ACE=90�㣬
���BAC+��ACB=��ACB+��ECM=90�㣬
���BAC=��ECM�����ACB�ס�ECM��
�� ![]() =k��
=k��
��BC=kEM��
ͬ����BCD�ס�NHC��
�� ![]() =K��
=K��
��BC=kHN��
��EM=HN��
�ڡ�NHT���EMT�У� 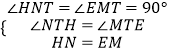 ��
��
���NHT�ա�EMT��
��ET=HT��
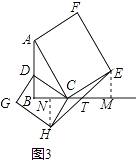
���������⣺��1���ߡ�MRN�ǵ���ֱ�������Σ�
��MR=RN����MRN=90�㣬
��MP��PQ��NQ��PQ��
���MPR=��NQ=90�㣬
���PMR+��MRP=��MRP+��NRQ=90�㣬
���PMR=��NRQ��
�ڡ�MPR���NRQ�У� 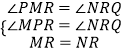 ��
��
���MPR�ա�NRQ��
��QN=PR����NRQ=��PMR��
���Դ��ǣ�PR����PMR��
�����㾫�������յ���ֱ�������κ�ȫ�������ε������ǽ����ĸ�������Ҫ֪������ֱ��������������ֱ�DZ���ȵ�ֱ�������Σ�����ֱ�������ε�����������ҵ���45�㣻ȫ�������εĶ�Ӧ�����; ȫ�������εĶ�Ӧ����ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һ����λ��n�����n���������λ�ϵ����ֻ�����ͬ���Ҷ���Ϊ�㣬��ô�������Ϊ��������������һ����������������������λ�ϵ����ֶԵ�����Եõ�������ͬ������λ����������������λ���ĺ���111���̼�ΪF��n��������n=123���Ե���λ��ʮλ�ϵ����ֵõ�213���Ե���λ���λ�ϵ����ֵõ�321���Ե�ʮλ���λ�ϵ����ֵõ�132������������λ���ĺ�Ϊ213+321+132=666��666��111=6������F��123��=6��
��1�����㣺F��243����F��617����
��2����s��t���ǡ���������������s=100x+32��t=150+y��1��x��9��1��y��9��x��y���������������涨��k= ![]() ����F��s��+F��t��=18ʱ����k�����ֵ��
����F��s��+F��t��=18ʱ����k�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABCD�У��Խ���AC��BD�ཻ�ڵ�O����AB=4��BD=10��sin��BDC= ![]() ����ABCD������� ��
����ABCD������� �� 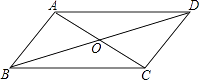
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=3��BC=4������P��A���������A��B��C�ķ�����AB��BC���ƶ�����PA=x����D��ֱ��PA�ľ���Ϊy����y����x�ĺ���ͼ������ǣ� ��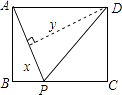
A.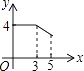
B.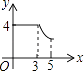
C.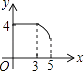
D.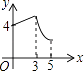
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=kx+b��k��0����˫����y= ![]() ��m��0���ཻ��A��1��2����B��n����1�����㣮
��m��0���ཻ��A��1��2����B��n����1�����㣮 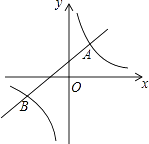
��1����˫���ߵĽ���ʽ��
��2����A1��x1 �� y1����A2��x2 �� y2����A3��x3 �� y3��Ϊ˫�����ϵ����㣬��x1��0��x2��x3 �� ��ֱ��д��y1 �� y2 �� y3�Ĵ�С��ϵ��
��3���۲�ͼ����ֱ��д������ʽkx+b�� ![]() �Ľ⼯��
�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABCD�У�AD=8cm��AB=6cm������E�ӵ�C��ʼ�ر�CB���B��2cm/s���ٶ��˶�������F�ӵ�Cͬʱ�����ر�CD���D��1cm/s���ٶ��˶�����Dֹͣ����ͼ�ɵõ�����CFHE�����˶�ʱ��Ϊx����λ��s������ʱ����ABCDȥ������CFHE��ʣ�ಿ�ֵ����Ϊy����λ��cm2������y��x֮��ĺ�����ϵ��ͼ���ʾ��������ͼ�еģ� ��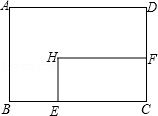
A.
B.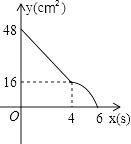
C.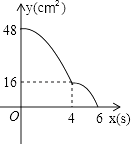
D.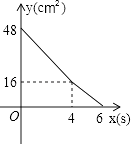
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ü�ˮ�����������г�����ij��ˮ�����ۣ���һ����1500Ԫ��������ǧ�ˣ�����ÿǧ��9Ԫ���ۣ��ܿ����꣮����ˮ���������ڶ��ι���ʱ��ÿǧ�˵Ľ��۱ȵ�һ�������10%����1694Ԫ�������ˮ���ȵ�һ�ζ�20ǧ�ˣ���ÿǧ��10Ԫ�۳�100ǧ�˺�����ָ���������ˮ�����ױ��ʣ�Ϊ������ʧ���㽵��45%����ʣ���ˮ����
(1)��һ��ˮ���Ľ�����ÿǧ�˶���Ԫ��
(2)��ˮ�����������������У���������ӯ�����ǿ���ӯ��������˶���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC�У���BAC=90�㣬����B��ֱ��MN��AC��DΪBC����һ�㣬����AD����DE��AD��MN�ڵ�E������AE��
��1����ͼ�٣�����ABC=45��ʱ����֤��AD=DE�� 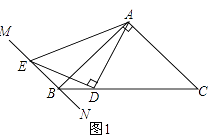
��2����ͼ�ڣ�����ABC=30��ʱ���߶�AD��DE�к�������ϵ������˵�����ɣ� 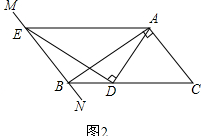
��3������ABC=��ʱ����ֱ��д���߶�AD��DE��������ϵ�����ú��������Ǻ�����ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��AOB�У���AOB=90�㣬OA��x���ϣ�OB��y���ϣ���A��B������ֱ�Ϊ�� ![]() ��0������0��1������Rt��AOB����AB���۵õ�Rt��AO��B�����O�������Ϊ ��
��0������0��1������Rt��AOB����AB���۵õ�Rt��AO��B�����O�������Ϊ �� 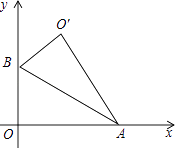
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com