
【题目】在Rt△ABC中,∠BAC=90°,过点B的直线MN∥AC,D为BC边上一点,连接AD,作DE⊥AD交MN于点E,连接AE.
(1)如图①,当∠ABC=45°时,求证:AD=DE; 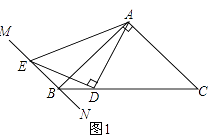
(2)如图②,当∠ABC=30°时,线段AD与DE有何数量关系?并请说明理由; 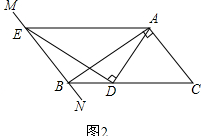
(3)当∠ABC=α时,请直接写出线段AD与DE的数量关系.(用含α的三角函数表示)
【答案】
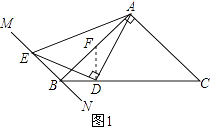
(1)证明:如图1,过点D作DF⊥BC,交AB于点F,
则∠BDE+∠FDE=90°,
∵DE⊥AD,
∴∠FDE+∠ADF=90°,
∴∠BDE=∠ADF,
∵∠BAC=90°,∠ABC=45°,
∴∠C=45°,
∵MN∥AC,
∴∠EBD=180°﹣∠C=135°,
∵∠BFD=45°,DF⊥BC,
∴∠BFD=45°,BD=DF,
∴∠AFD=135°,
∴∠EBD=∠AFD,
在△BDE和△FDA中
 ,
,
∴△BDE≌△FDA(ASA),
∴AD=DE
(2)解:DE= ![]() AD,
AD,
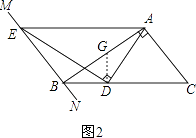
理由:如图2,过点D作DG⊥BC,交AB于点G,
则∠BDE+∠GDE=90°,
∵DE⊥AD,
∴∠GDE+∠ADG=90°,
∴∠BDE=∠ADG,
∵∠BAC=90°,∠ABC=30°,
∴∠C=60°,
∵MN∥AC,
∴∠EBD=180°﹣∠C=120°,
∵∠ABC=30°,DG⊥BC,
∴∠BGD=60°,
∴∠AGD=120°,
∴∠EBD=∠AGD,
∴△BDE∽△GDA,
∴ ![]() =
= ![]() ,
,
在Rt△BDG中,
![]() =tan30°=
=tan30°= ![]() ,
,
∴DE= ![]() AD
AD
(3)AD=DEtanα;
理由:如图2,∠BDE+∠GDE=90°,
∵DE⊥AD,
∴∠GDE+∠ADG=90°,
∴∠BDE=∠ADG,
∵∠EBD=90°+α,∠AGD=90°+α,
∴∠EBD=∠AGD,
∴△EBD∽△AGD,
∴ ![]() =
= ![]() ,
,
在Rt△BDG中,
![]() =tanα,则
=tanα,则 ![]() =tanα,
=tanα,
∴AD=DEtanα

【解析】(1)首先过点D作DF⊥BC,交AB于点F,得出∠BDE=∠ADF,以及∠EBD=∠AFD,再得出△BDE≌△FDA(ASA),求出即可;(2)首先过点D作DG⊥BC,交AB于点G,进而得出∠EBD=∠AGD,证出△BDE∽△GDA即可得出答案;(3)首先过点D作DG⊥BC,交AB于点G,进而得出∠EBD=∠AGD,证出△BDE∽△GDA即可得出答案.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】(1)如图,已知点C在线段AB上,且AC=5cm,BC=3cm,点M,N分别是AC,BC的中点,求线段MN的长度.
(2)若点C是线段AB上任意一点,且AC=a,BC=b, 点M、N分别是,AC,BC的中点,请直接写出线段MN的长度(用含a,b的代数式表示)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将含45°角的三角板的直角顶点R放在直线l上,分别过两锐角的顶点M,N作l的垂线,垂足分别为P、Q,
(1)如图1,观察图1可知:与NQ相等的线段是 , 与∠NPQ相等的角是 . 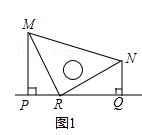
(2)直角△ABC中,∠B=90°,在AB边上任取一点D,连接CD,分别以AC,DC为边作正方形ACEF和正方形CDGH,如图2,过E,H分别作BC所在直线的垂线,垂足分别为K,L.试探究EK与HL之间的数量关系,并证明你的结论.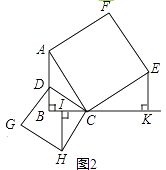
(3)直角△ABC中,∠B=90°,在AB边上任取一点D,连接CD,分别以AC,DC为边作矩形ACEF和矩形CDGH,连接EH交BC所在的直线于点T,如图3,如果AC=kCE,CD=kCH,试探究TE与TH之间的数量关系,并证明你的结论.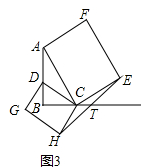
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,其中从第三个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的长度构造一组正方形(如下图),再分别依次从左到右取2个,3个,4个,5个正方形拼成如下长方形并记为①,②,③,④,相应长方形的周长如下表所示:
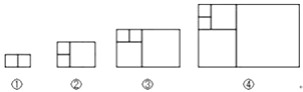

若按此规律继续作长方形,则序号为⑧的长方形周长是( )
A. 288 B. 178 C. 28 D. 110
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45°;②AG+DF=FG;③△DEF∽△ABG;④S△ABG= ![]() S△FGH . 其中正确的是( )
S△FGH . 其中正确的是( ) 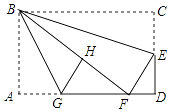
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列各题:
(1)如图,已知直线AB与⊙O相切于点C,且AC=BC,求证:OA=OB. 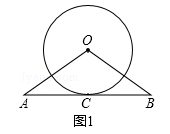
(2)如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AB=3,求AC的长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OA⊥OB,∠AOD=∠BOC由此判定OC⊥OD,下面是推理过程,请填空.

解:∵OA⊥OB(已知)
所以_____=90°(________)
因为_____=∠AOD-∠AOC,____=∠BOC-∠AOC,∠AOD=∠BOC,
所以______=_____(等量代换)
所以______=90°
所以OC⊥OD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com