
【题目】小强是校学生会体育部部长,他想了解现在同学们更喜欢什么球类运动,以便学生会组织受欢迎的比赛.于是他设计了调查问卷,在全校每个班都随机选取了一定数量的学生进行调查,调查问卷如下:
调查问卷
你最喜欢的球类运动是( )(单选)
A、篮球B、足球C、排球D、乒乓球E、羽毛球F、其他
调查问卷
你最喜欢的球类运动是( )(单选)
A、篮球B、足球C、排球D、乒乓球E、羽毛球F、其他
小强根据统计数据制作的各活动小组人数分布情况的统计表和扇形统计图如下
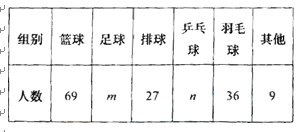

(1)请你写出统计表中空缺部分的人数m= , n= .
(2)在扇形统计图中,羽毛球所对应的扇形圆心角等于 .
(3)请你根据调查结果,给小强部长简要提出两条合理化的建议.
【答案】(1)m=63,n=96;(2)43.2;(3)①多组织执行乒乓球比赛 ②少组织排球比赛
【解析】
(1)根据篮球人数占总人数23%求出被调查的总人数,将总人数分别乘以足球和乒乓球的百分比,可得m、n的值;
(2)根据羽毛球所对应扇形的圆心角等于羽毛球人数占总人数的比例乘以360°可得;
(3)根据喜欢不同球类人数多少可选择多开展相应的活动,合理即可.
(1)根据题意知,被调查的学生一共有:69÷23%=300人,
则选择足球的人数m=300×21%=63人,选择乒乓球的人数n=300-69-63-27-36-9=96人;
故答案为:63,96;
(2)羽毛球所对应扇形的圆心角为:![]() ×360°=43.2°;
×360°=43.2°;
(3)因为喜欢乒乓球和羽毛球的人数最多,所以①多组织执行乒乓球比赛;②少组织排球比赛.
故答案为:(1)63,96;(2)43.2°.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径画弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①BE= ![]() AC;②∠A=∠EBA;③EB平分∠AED;④ED=
AC;②∠A=∠EBA;③EB平分∠AED;④ED= ![]() AB中,一定正确的是( )
AB中,一定正确的是( ) 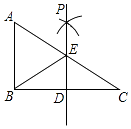
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
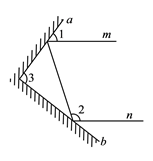
【题目】实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
(1)如图,一束光线![]() 射到平面镜
射到平面镜![]() 上,被
上,被![]() 反射到平面镜
反射到平面镜![]() 上,又被
上,又被![]() 反射,若被
反射,若被![]() 反射出的光线
反射出的光线![]() 与光线
与光线![]() 平行,且
平行,且![]() ,则
,则![]() _________,
_________,![]() ________.
________.
(2)在(1)中,若![]() ,则
,则![]() _______;若
_______;若![]() ,则
,则![]() ________;
________;
(3)由(1)、(2),请你猜想:当两平面镜![]() 、
、![]() 的夹角
的夹角![]() ________时,可以使任何射到平面镜
________时,可以使任何射到平面镜![]() 上的光线
上的光线![]() ,经过平面镜
,经过平面镜![]() 、
、![]() 的两次反射后,入射光线
的两次反射后,入射光线![]() 与反射光线
与反射光线![]() 平行.请说明理由.
平行.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
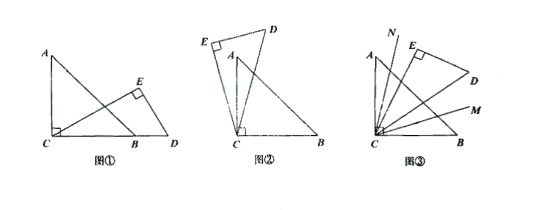
【题目】如图,将一个直角三角板中30°的锐角顶点与另一个直角三角板的直角顶点叠放一起.(注:∠ACB与∠DEC是直角,∠A=45°,∠DEC=30°).
(1)如图①,若点C、B、D在一条直线上,求∠ACE的度数;
(2)如图②,将直角三角板CDE绕点c逆时针方向转动到某个位置,若恰好平分∠DCE,求∠BCD的度数;
(3)如图③若∠DEC始终在∠ACB的内部,分别作射线CM平分∠BCD,射线CN平分∠ACE.如果三角板DCE在∠ACB内绕点C任意转动,∠MCN的度数是否发生变化?如果不变,求出它的度数,如果变化,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.
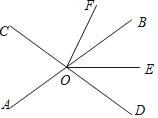
(1)若∠AOC=76°,求∠BOF的度数;
(2)若∠BOF=36°,求∠AOC的度数;
(3)若|∠AOC﹣∠BOF|=α°,请直接写出∠AOC和∠BOF的度数.(用含的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为原点,平行四边形ABCD的边BC在x轴上,D点在y轴上,C点坐标为(2,0),BC=6,∠BCD=60°,点E是AB上一点,AE=3EB,⊙P过D,O,C三点,抛物线y=ax2+bx+c过点D,B,C三点.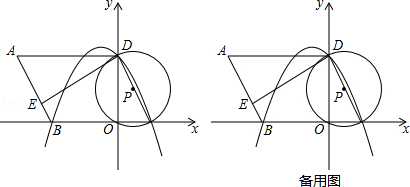
(1)求抛物线的解析式;
(2)说明ED是⊙P的切线,若将△ADE绕点D逆时针旋转90°,E点的对应点E′会落在抛物线上吗?请说明理由;
(3)若点M为此抛物线的顶点,平面上是否存在点N,使得以点B,D,M,N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com