
【题目】不等式组 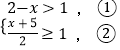 中,不等式①和②的解集在数轴上表示正确的是( )
中,不等式①和②的解集在数轴上表示正确的是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:解不等式①,得:x<1,
解不等式②,得:x≥﹣3,
则不等式组的解集为﹣3≤x<1,
故选:B.
【考点精析】关于本题考查的不等式的解集在数轴上的表示和一元一次不等式组的解法,需要了解不等式的解集可以在数轴上表示,分三步进行:①画数轴②定界点③定方向.规律:用数轴表示不等式的解集,应记住下面的规律:大于向右画,小于向左画,等于用实心圆点,不等于用空心圆圈;解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )才能得出正确答案.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
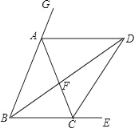
【题目】如图,已知在△ABC中,AD、BD分别平分∠CAG、∠EBA,AD∥BC,BD交AC于F,连接CD,
(1)求证:AB=AC.
(2)当∠EBA的大小满足什么条件时,以A,B,F为顶点三角形为等腰三角形?
(3)猜想∠BDC与∠DAC之间的数量关系式,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC=BC,点E是AC上一点,连接BE. 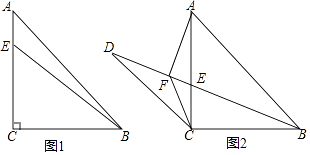
(1)如图1,若AB=4 ![]() ,BE=5,求AE的长;
,BE=5,求AE的长;
(2)如图2,点D是线段BE延长线上一点,过点A作AF⊥BD于点F,连接CD、CF,当AF=DF时,求证:DC=BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜3个、乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.
(1)甲、乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请设计几种购买方案供这个学校选择.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+b(k≠0)的图象经过点A(2,﹣6),且与反比例函数y=﹣ ![]() 的图象交于点B(a,4)
的图象交于点B(a,4)
(1)求一次函数的解析式;
(2)将直线AB向上平移10个单位后得到直线l:y1=k1x+b1(k1≠0),l与反比例函数y2= ![]() 的图象相交,求使y1<y2成立的x的取值范围.
的图象相交,求使y1<y2成立的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强是校学生会体育部部长,他想了解现在同学们更喜欢什么球类运动,以便学生会组织受欢迎的比赛.于是他设计了调查问卷,在全校每个班都随机选取了一定数量的学生进行调查,调查问卷如下:
调查问卷
你最喜欢的球类运动是( )(单选)
A、篮球B、足球C、排球D、乒乓球E、羽毛球F、其他
调查问卷
你最喜欢的球类运动是( )(单选)
A、篮球B、足球C、排球D、乒乓球E、羽毛球F、其他
小强根据统计数据制作的各活动小组人数分布情况的统计表和扇形统计图如下
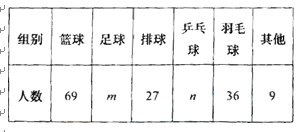

(1)请你写出统计表中空缺部分的人数m= , n= .
(2)在扇形统计图中,羽毛球所对应的扇形圆心角等于 .
(3)请你根据调查结果,给小强部长简要提出两条合理化的建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数y= ![]() (x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )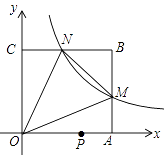
A.6 ![]()
B.10
C.2 ![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中, △ABC三个顶点的位置如图(每个小正方形的边长均为1).
(1)请画出△ABC沿x轴向右平移3个单位长度,再沿y轴向下平移2个单位长度后的△A′B′C′(其中A′、B′、C′分别是A、B、C的对应点,不写画法)
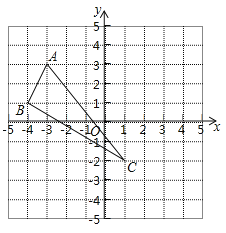
(2)直接写出A′、B′、C′三点的坐标:
A′(_____,______); B′(_____,______);
C′(_____,______).
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某股民上周五购进某公司股票500股,每股30元.(星期六、星期日封盘,关闭交易)下表是本周内每日该股票比前一天的涨跌情况(单位:元)

星期一,星期二被墨水污染,只知道星期一比上周五上涨10%,星期二比星期一下跌10%.根据以上信息,请回答:
(1)星期三收盘时,每股是多少元?
(2)本周内每股最高价是多少元?最低价是多少元?
(3)已知该股民购进股票时付了1.5‰的手续费,卖出时还要付成交额1.5‰的手续费和1‰的交易税.如果他在星期五收盘时全部卖出该股票,他是赚钱还是亏本?赚或亏了多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com